
【题目】数学活动:擦出智慧的火花---------由特殊到一般的数学思想.
数学课上,李老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC上的点,过点E作EF⊥AE,过点F作FG⊥BC交BC的延长线于点G..
(1)求证:∠BAE=∠FEG.
(2)同学们很快做出了解答,之后李老师将题目修改成:如图2,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.请借助图1完成小明的证明;
在(2)的基础上,同学们作了进一步的研究:
(3)小聪提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小聪的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;


【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】试题分析:(1)根据∠AEF=90°,即可得到∠AEB+∠FEG=90°,在直角△ABE中,利用三角形内角和定理得到∠BAE+∠AEB=90°,然后根据同角的余角相等,即可证得;
(2)作AB的中点M,连接ME,根据ASA即可证明△AME≌△ECF,然后根据全等三角形的对应边相等即可证得;
(3)在AB上取一点M,使AM=EC,连接ME,同(2)根据ASA即可证明△AME≌△ECF,然后根据全等三角形的对应边相等即可证得.
试题解析:解:(1)∵∠AEF=90°,∴∠AEB+∠FEG=90°.又∵直角△ABE中,∠BAE+∠AEB=90°,∴∠BAE=∠FEG;
(2)作AB的中点M,连接ME.
∵正方形ABCD中,AB=BC.又∵AM=MB=![]() AB,BE=CE=
AB,BE=CE=![]() BC,∴MB=BE,∴△MBE是等腰直角三角形,∴∠BME=45°,∴∠AME=135°.又∵∠ECF=180°﹣∠FCG=180°﹣45°=135°,∴∠AME=∠ECF.在△AME和△ECF中,∵∠BAE=∠FEC,AM=EC,∠AME=∠ECF,∴△AME≌△ECF,∴AE=EF;
BC,∴MB=BE,∴△MBE是等腰直角三角形,∴∠BME=45°,∴∠AME=135°.又∵∠ECF=180°﹣∠FCG=180°﹣45°=135°,∴∠AME=∠ECF.在△AME和△ECF中,∵∠BAE=∠FEC,AM=EC,∠AME=∠ECF,∴△AME≌△ECF,∴AE=EF;
(3)在AB上取一点M,使AM=EC,连接ME,∴BM=BE,∴∠BME=45°,∴∠AME=135°.∵CF是外角平分线,∴∠DCF=45°,∴∠ECF=135°,∴∠AME=∠ECF.
∵∠AEB+∠BAE=90°,∠AEB+∠CEF=90°,∴∠BAE=∠CEF.在△AME和△ECF中,∵∠BAE=∠FEC,AAM=EC,∠AME=∠ECF,∴△AME≌△ECF(ASA),∴AE=EF.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4,2)、B(0,4)、C(0,2),

(1)画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④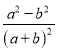 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);
(2)若![]() 为正整数,且
为正整数,且![]() 为“和谐分式”,请写出
为“和谐分式”,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小东和小强分别进行了如下三步变形:
小东: ![]()
![]()
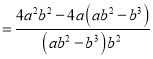
小强: ![]()
![]()
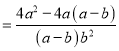
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若OC是∠AOB内部的一条射线,则下列式子中,不能表示“OC是∠AOB的平分线”的是( )
A. ∠AOC=∠BOC B. ∠AOB=2∠BOC
C. ∠AOC=![]() ∠AOB D. ∠AOC+∠BOC=∠AOB
∠AOB D. ∠AOC+∠BOC=∠AOB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,某班同学用天平和一些物品(如图)探究了等式的基本性质.该班科技创新小组的同学提出问题:仅用一架天平和一个10克的砝码能否测量出乒乓球和一次性纸杯的质量?科技创新小组的同学找来足够多的乒乓球和某种一次性纸杯(假设每个乒乓球的质量相同,每个纸杯的质量也相同),经过多次试验得到以下记录:

记录 | 天平左边 | 天平右边 | 状态 |
记录一 | 6个乒乓球, 1个10克的砝码 | 14个一次性纸杯 | 平衡 |
记录二 | 8个乒乓球 | 7个一次性纸杯, 1个10克的砝码 | 平衡 |
请算一算,一个乒乓球的质量是多少克?一个这种一次性纸杯的质量是多少克?
解:(1)设一个乒乓球的质量是![]() 克,则一个这种一次性纸杯的质量是______克;(用含
克,则一个这种一次性纸杯的质量是______克;(用含![]() 的代数式表示)
的代数式表示)
(2)列一元一次方程求一个乒乓球的质量,并求出一个这种一次性纸杯的质量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD 中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N ,连接OM,ON,MN .下列五个结论:①△CNB≌△DMC ;②△CON≌△DOM ;③△OMN≌△OAD ;④![]() ;⑤若AB=2,则
;⑤若AB=2,则![]() 的最小值是
的最小值是![]() ,其中正确结论的个数是 ( )
,其中正确结论的个数是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上的位置如图所示:
![]()
(1)点A表示的数是 ,点B表示的数是 ;
(2)在原图中分别标出表示+1.5的点C、表示﹣3.5的点D;
(3)在上述条件下,B、C两点间的距离是 ,A、C两点间的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B对应的数分别为-1、4,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、点B的距离相等,则点P对应的数是_____;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为8?若存在,请直接写出x的值,若不存在,请说明理由;
(3)现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,点P以5个单位长度/秒的速度同时从O点(即原点)向左运动,当点A与点B之间的距离为3个单位长度时,求点P所对应的数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com