
【题目】已知数轴上两点A、B对应的数分别为-1、4,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、点B的距离相等,则点P对应的数是_____;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为8?若存在,请直接写出x的值,若不存在,请说明理由;
(3)现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,点P以5个单位长度/秒的速度同时从O点(即原点)向左运动,当点A与点B之间的距离为3个单位长度时,求点P所对应的数是多少?
【答案】(1)1.5;(2)当x=-2.5或5.5时,满足点P到点A、点B的距离之和为8;(3)点P所对应的数是-6![]() 或-32.
或-32.
【解析】
(1)由点P到点A、点B的距离相等得点P是线段AB的中点,而A、B对应的数分别为-1、3,根据数轴即可确定点P对应的数;
(2)分两种情况讨论:①当点P在A左边时;②点P在B点右边时;分别求出x的值即可.
(3)分两种情况讨论:①当点A在点B左边两点相距3个单位时;②当点A在点B右边时,两点相距3个单位时;分别求出t的值,然后求出点P对应的数即可.
(1)∵点P到点A、点B的距离相等,
∴点P是线段AB的中点,
∵点A、B对应的数分别为-1、4
∴点P对应的数是1.5.
故答案是:1.5;
(2)①当点P在A左边时,-1-x+4-x=8,
解得:x=-2.5;
②点P在B点右边时,x-4+x-(-1)=8,
解得:x=5.5,
即存在x的值,当x=-2.5或5.5时,满足点P到点A、点B的距离之和为8;
(3)①当点A在点B左边两点相距3个单位时,此时需要的时间为t,
则4+0.5t-(2t-1)=3,
解得:t=![]() ,
,
则点P对应的数为-5×![]() =-
=-![]() =-6
=-6![]() ;
;
②当点A在点B右边两点相距3个单位时,此时需要的时间为t,
则2t-1-(4+0.5t)=3,1.5t=8
得:t=![]() ,
,
则点P对应的数为-6×![]() =-32;
=-32;
综上可得当点A与点B之间的距离为3个单位长度时,点P所对应的数是-6![]() 或-32.
或-32.


科目:初中数学 来源: 题型:
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为12cm,点B,D之间的距离为16m,则线段AB的长为![]()
![]()

A. ![]() B. 10cmC. 20cmD. 12cm
B. 10cmC. 20cmD. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动:擦出智慧的火花---------由特殊到一般的数学思想.
数学课上,李老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC上的点,过点E作EF⊥AE,过点F作FG⊥BC交BC的延长线于点G..
(1)求证:∠BAE=∠FEG.
(2)同学们很快做出了解答,之后李老师将题目修改成:如图2,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.请借助图1完成小明的证明;
在(2)的基础上,同学们作了进一步的研究:
(3)小聪提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小聪的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,两个圈分别表示负数集和分数集. 请你把下列各数填入表示它所在的数集的圈里:
-50% , 2011 , 0.618 , -3 ,![]() ,0 , 5.9,-3.14 , -92 .
,0 , 5.9,-3.14 , -92 .

(2)图中,这两个圈的重叠部分表示什么数的集合?
(3)在(1)的数据中,求最大的数与最小的数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在面积为60的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=10,BC=12,则CE+CF的值为( )
A. 22-11![]() B.
B. ![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
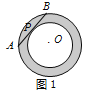
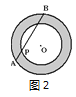
【题目】(1)如图1,同心圆中,大圆O的弦AB与小圆O切于点P,且AB=16,则圆环面积为________;
(2)如图2,同心圆中,大圆O的弦AB与小圆O相交,其中一个交点为点P,且AP=2,PB=8,则圆环面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
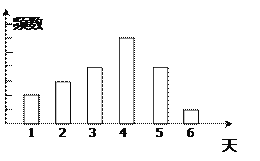
【题目】某公司对用户满意度进行问卷调查,将连续6天内每天收回的问卷数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第3天的频数是12.请你回答:
(1)收回问卷最多的一天共收到问卷_________份;
(2)本次活动共收回问卷共_________份;
(3)市场部对收回的问卷统一进行了编号,通过电脑程序随机抽选一个编号,抽到问卷是第4天收回的概率是多少?
(4)按照(3)中的模式随机抽选若干编号,确定幸运用户发放纪念奖,第4天和第6天分别有10份和2份获奖,那么你认为这两组中哪个组获奖率较高?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
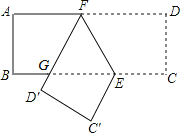
【题目】如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为______(用含t的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com