
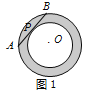
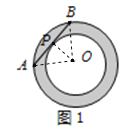
【题目】(1)如图1,同心圆中,大圆O的弦AB与小圆O切于点P,且AB=16,则圆环面积为________;
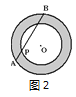
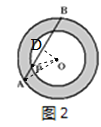
(2)如图2,同心圆中,大圆O的弦AB与小圆O相交,其中一个交点为点P,且AP=2,PB=8,则圆环面积为________.
【答案】 ![]()
![]()
【解析】分析:(1)根据圆环的面积等于两圆的面积差,再根据切线的性质定理、勾股定理、垂径定理求解;
(2)根据圆环的面积等于两圆的面积差,再根据垂径定理、勾股定理求解即可.
详解:(1)连接OA、OB、OP.
∵大圆的弦AB是小圆的切线,∴OP⊥AB,AP=PB,∴OB2﹣OP2=(16÷2)2=64.
∵S圆环=S大﹣S小=πOB2﹣πOP2=π(OB2﹣OP2),∴S圆环=64π.
(2)过O作OD⊥AB于D,连接OP,OA.
∵AP=2,PB=8,∴AB=10.
∵OD⊥AB,∴AD=![]() AB=5.
AB=5.
∵AP=2,∴PD=3.
在Rt△AOD和Rt△POD中,
∵OA2=AD2+OD2,OP2=PD2+OD2,∴OA2-OP2= AD2-PD2= 52-32=16.
S圆环=S大﹣S小=πOA2﹣πOP2=π(OA2﹣OP2),∴S圆环=16π.
故答案为:(1)64π;(2)16π.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
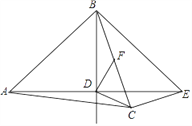
(1)若BD=DE=![]() ,CE=
,CE=![]() ,求BC的长;
,求BC的长;
(2)若BD=DE,求证:BF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD 中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N ,连接OM,ON,MN .下列五个结论:①△CNB≌△DMC ;②△CON≌△DOM ;③△OMN≌△OAD ;④![]() ;⑤若AB=2,则
;⑤若AB=2,则![]() 的最小值是
的最小值是![]() ,其中正确结论的个数是 ( )
,其中正确结论的个数是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠C=90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,但须保留作图痕迹).
(2)已知内角度数的两个三角形如图2,图3所示.请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B对应的数分别为-1、4,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、点B的距离相等,则点P对应的数是_____;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为8?若存在,请直接写出x的值,若不存在,请说明理由;
(3)现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,点P以5个单位长度/秒的速度同时从O点(即原点)向左运动,当点A与点B之间的距离为3个单位长度时,求点P所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用如图所示矩形纸片的四个角都剪去一个边长为![]() 的正方形(阴影部分).并制成一个长方体纸盒。
的正方形(阴影部分).并制成一个长方体纸盒。
(1)用a,b,x表示纸片剩余部分的面积和纸盒的底面积;
(2)当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
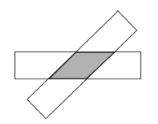
【题目】(1)将两条宽度一样的矩形纸条如图交叉,请判断重叠部分是一个什么图形?并证明你的结论。
(2) 若两张矩形纸条的长度均为8,宽度均为2,请求出重叠部分的图形的周长的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,AD=6,DC=7,点H为AD上一点,并且AH=2,点E为AB上一动点,以HE为边长作菱形HEFG,并且使点G在CD边上,连接CF
(1)如图1,当DG=2时,求证:四边形EFGH为正方形;
(2)如图2,当DG=6时,求△CGF的面积;
(3)当DG的长度为何值时,△CGF的面积最小,并求出△CGF面积的最小值;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上☆○☆,B组的卡片上分别画上☆○○,如图1所示.
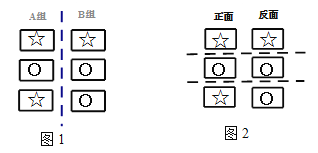
(1)若将卡片无标记的一面朝上摆在桌上,再分别从两组卡片中随机各抽取一张,求两张卡片上标记都是☆的概率(请用画树形图法或列表法求解)
(2)若把A,B两组卡片无标记的一面对应粘贴在一起得到3张卡片,其正反面标记如图2所示,将卡片正面朝上摆放在桌上,并用瓶盖盖住标记.若揭开盖子,看到的卡片正面标记是☆后,猜想它的反面也是☆,求猜对的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com