
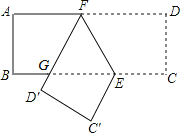
【题目】如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为______(用含t的代数式表示).
【答案】2![]() t
t
【解析】
根据翻折的性质可得CE=C′E,再根据直角三角形30°角所对的直角边等于斜边的一半判断出∠EBC′=30°,然后求出∠BGD′=60°,根据对顶角相等可得∠FGE=∠∠BGD′=60°,根据两直线平行,内错角相等可得∠AFG=∠FGE,再求出∠EFG=60°,然后判断出△EFG是等边三角形,根据等边三角形的性质表示出EF,即可得解.
解:由翻折的性质得,CE=C′E,

∵BE=2CE,
∴BE=2C′E,
又∵∠C′=∠C=90°,
∴∠EBC′=30°,
∵∠FD′C′=∠D=90°,
∴∠BGD′=60°,
∴∠FGE=∠BGD′=60°,
∵AD∥BC,
∴∠AFG=∠FGE=60°,
∴∠EFG=![]() (180°-∠AFG)=
(180°-∠AFG)=![]() (180°-60°)=60°,
(180°-60°)=60°,
∴△EFG是等边三角形,
∵AB=t,
∴EF=t÷![]() ,
,
∴△EFG的周长=![]() .
.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B对应的数分别为-1、4,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、点B的距离相等,则点P对应的数是_____;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为8?若存在,请直接写出x的值,若不存在,请说明理由;
(3)现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,点P以5个单位长度/秒的速度同时从O点(即原点)向左运动,当点A与点B之间的距离为3个单位长度时,求点P所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,某商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果红旗商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是 ( )

A. (![]() ,3)、(﹣
,3)、(﹣![]() ,4) B. (
,4) B. (![]() ,3)、(﹣
,3)、(﹣![]() ,4)
,4)
C. (![]() ,
,![]() )、(﹣
)、(﹣![]() ,4) D. (
,4) D. (![]() ,
,![]() )、(﹣
)、(﹣![]() ,4)
,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有六张完全相同的卡片,分A,B两组,每组三张,在A组的卡片上分别画上☆○☆,B组的卡片上分别画上☆○○,如图1所示.
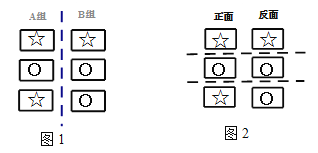
(1)若将卡片无标记的一面朝上摆在桌上,再分别从两组卡片中随机各抽取一张,求两张卡片上标记都是☆的概率(请用画树形图法或列表法求解)
(2)若把A,B两组卡片无标记的一面对应粘贴在一起得到3张卡片,其正反面标记如图2所示,将卡片正面朝上摆放在桌上,并用瓶盖盖住标记.若揭开盖子,看到的卡片正面标记是☆后,猜想它的反面也是☆,求猜对的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加x元.求:
(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)该宾馆每天的房间收费z(元)关于x(元)的函数关系式;
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F,若四边形DCFE的周长为18cm,AC的长6cm,则AD的长为( )

A. 13cmB. 12cmC. 5cmD. 8cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com