练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】点A、B在数轴上的位置如图所示：

    （1）点A表示的数是　 　，点B表示的数是　 　；

    （2）在原图中分别标出表示+1.5的点C、表示﹣3.5的点D；

    （3）在上述条件下，B、C两点间的距离是　 　，A、C两点间的距离是　 　．

    【答案】（1）﹣2，3；（2）见解析（3）1.5，3.5．

    【解析】

    （1）根据数轴上点的位置找出A与B表示的点即可；
    （2）在数轴上找出表示+1.5与﹣3.5的两个点C与D即可；
    （3）找出B、C之间的距离，以及A，C之间的距离即可．

    （1）点A表示的数是﹣2，点B表示的数是3．故答案为：﹣2，3；

    （2）如图，

    （3）在上述条件下，B、C两点间的距离是：3﹣1.5＝1.5，A、C两点间的距离是：1.5﹣（﹣2）＝3.5，

    故答案为：1.5，3.5．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

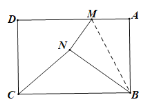
    【题目】如图，矩形纸片ABCD中，AD＝5，AB＝3．若M为射线AD上的一个动点，将△ABM沿BM折叠得到△NBM．若△NBC是直角三角形．则所有符合条件的M点所对应的AM长度的和为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝ax2＋bx＋c（a≠0）的图象如图所示，有下列5个结论： ① c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am+bm+a＞0（m≠﹣1）；⑤设A（100，y），B（﹣100，y）在该抛物线上，则y＞y．其中正确的结论有___________ ．（写出所有正确结论的序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学活动：擦出智慧的火花---------由特殊到一般的数学思想．

    数学课上，李老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC上的点，过点E作EF⊥AE,过点F作FG⊥BC交BC的延长线于点G..

    （1）求证：∠BAE=∠FEG.

    （2）同学们很快做出了解答，之后李老师将题目修改成：如图2，四边形ABCD是正方形，点E是边BC的中点．∠AEF=90°，且EF交正方形外角∠DCG的平分线于点F，求证：AE=EF．

    经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证△AME≌△ECF，所以AE＝EF．请借助图1完成小明的证明；

    在（2）的基础上，同学们作了进一步的研究：

    （3）小聪提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小聪的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BI，CI分别平分∠ABC，∠ACB，过I点作DE∥BC，交AB于D，交AC于E，给出下列结论：①△DBI是等腰三角形；②△ACI是等腰三角形；③AI平分∠BAC；④△ADE周长等于AB＋AC.其中正确的是(　　)

    A. ①②③ B. ②③④ C. ①③④ D. ①②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图，两个圈分别表示负数集和分数集. 请你把下列各数填入表示它所在的数集的圈里：

    -50% ， 2011 ， 0.618 ， -3 ， ，0 ， 5.9，-3.14 ， -92 .

    （2）图中，这两个圈的重叠部分表示什么数的集合？

    （3）在（1）的数据中，求最大的数与最小的数之和.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在面积为60的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F，若AB=10，BC=12，则CE+CF的值为（ ）

    A. 22-11B.

    C. 或D. 或

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=6，BC=4，过对角线BD中点O的直线分别交AB，CD边于点E，F．

    （1）求证：四边形BEDF是平行四边形；

    （2）当四边形BEDF是菱形时，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知两点、在数轴上，，点表示的数是，且与互为相反数．

    （1）写出点表示的数；

    （2）如图1，当点、位于原点的同侧时，动点、分别从点、处在数轴上同时相向而行，动点的速度是动点的速度的2倍，3秒后两动点相遇，当动点到达点4时，运动停止．在整个运动过程中，当时，求点、所表示的数；

    （3）如图2，当点、位于原点的异侧时，动点、分别从点、处在数轴上向右运动，动点比动点晚出发1秒；当动点运动2秒后，动点到达点处，此时动点立即掉头以原速向左运动3秒恰与动点相遇；相遇后动点又立即掉头以原速向右运动5秒，此时动点到达点处，动点到达点处,当时，求动点、运动的速度．

    查看答案和解析>>

    同步练习册答案