
【题目】如图1,直线l : ![]() 经过定点P,交x、y轴于A、B两点.
经过定点P,交x、y轴于A、B两点.
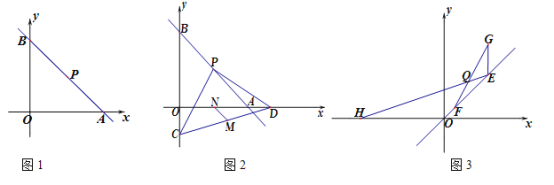
(1)如图1,直接写出点P的坐标__________________;
(2)如图2,当k=—1时,点C为y轴负半轴上一动点,过点P作PD⊥PC交x轴于点D,M、N分别为CD、OA的中点,求![]() 的值;
的值;
(3)如图3,E、F两点在射线OP上移动,EF=![]() ,点E向上移动2个单位得到点G,点E横坐标为 t(t>0),在x轴负半轴上有点H(—2t,0),FG与HE相交于Q点,求证:点Q在某条直线上运动,并求此直线的解析式.
,点E向上移动2个单位得到点G,点E横坐标为 t(t>0),在x轴负半轴上有点H(—2t,0),FG与HE相交于Q点,求证:点Q在某条直线上运动,并求此直线的解析式.
【答案】(1)(2,2);(2)![]() ;(3)点Q在直线
;(3)点Q在直线![]() 上运动.
上运动.
【解析】
(1)将直线l解析式变形可得到定点坐标;
(2)过点P作EF∥x轴,过点D作DF⊥EF垂足为F,首先证明△EPC≌△FDP,设C(0,m),则PF=CE=2-m,易得D(4-m,0),然后根据k=-1求出A点坐标,可得AD=-m,利用中点坐标公式和两点间距离公式求出MN,问题得解;
(3)如图3,延长GE交x轴于点J,则GJ⊥x轴,过点F作FK⊥GJ于点K,由OP所以直线解析式为y=x,可求得F点、G点坐标,然后用待定系数法求出直线HE和直线FG解析式,求出交点Q的坐标,即可解得点Q在直线![]() 上运动.
上运动.
解:(1)∵![]() ,
,
∴当x=2时,y=2,
∴定点P的坐标是(2,2);
(2)如图2,过点P作EF∥x轴,过点D作DF⊥EF垂足为F,
∵P(2,2),∴PE=OE=DF=2,
∵PD⊥PC,
∴∠EPC+∠FPD=90°,
∵∠EPC+∠ECP=90°,
∴∠FPD=∠ECP,
在△EPC和△FDP中,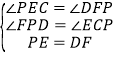 ,
,
∴△EPC≌△FDP(AAS),
∴PF=CE,
设C(0,m),则PF=CE=2-m,
∴OD=PE+PF=4-m,
∴D(4-m,0),
当k=-1时,直线l解析式为:![]() ,
,
∴A(4,0),AD=-m,
∵M、N分别为CD、OA的中点,
∴M(![]() ,
,![]() ),N(2,0),
),N(2,0),
∴MN=![]() ,
,
∴![]() ;
;
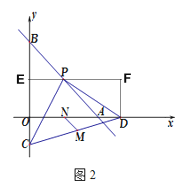
(3)如图3,延长GE交x轴于点J,则GJ⊥x轴,过点F作FK⊥GJ于点K,
∵E、F两点在射线OP上移动且P(2,2),
∴OP所以直线解析式为:y=x,
∴∠EOJ=∠EFK =45°,
∵EF=![]() ,
,
∴EK=FK=EG=2,
∵E(t,t),
∴G(t,t+2),F(t-2,t-2),
设直线HE解析式为:y=kx+b(k≠0),
将点E(t,t),H(-2t,0)代入可得:![]() ,
,
解得: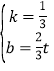 ,
,
∴直线HE解析式为:y=![]() x+
x+![]() ,
,
设直线FG解析式为:y=k1x+b1(k≠0),
将点 G(t,t+2),F(t-2,t-2)代入可得:![]() ,
,
解得:![]() ,
,
∴直线FG解析式为:y=2x+2-t,
联立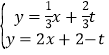 ,解得:
,解得: ,
,
即Q(![]() ,
,![]() ),
),
∵![]() ,
,
∴点Q在直线![]() 上运动.
上运动.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】长为1,宽为a的矩形纸片(![]() ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为( )
),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为( )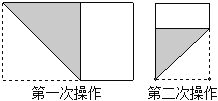
查看答案和解析>>
科目:初中数学 来源: 题型:
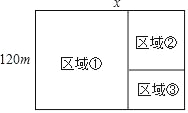
【题目】如图所示,某校在开发区一块宽为120m的矩形用地上新建分校区,规划图纸上把它分成①②③三个区域,区域①和区域②为正方形,区域①为教学区;区域②为生活区;区域③为活动区,设这块用地长为xm,区域③的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)若区域③的面积为3200m2,那么这块用地的长应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,则图3中共有7个正方形;……如此剪下去,则第n个图形中正方形的个数是多少?

(1)将下表填写完整:
图(n) | 1 | 2 | 3 | 4 | 5 | …… | n |
正方形的个数 | 1 | 4 | 7 | …… | an |
(2)an= (用含n的代数式表示)
(3)按照上述方法,能否得到2019个正方形?如果能,请求出n;如果不能,请简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4,2)、B(0,4)、C(0,2),

(1)画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP
(2)如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的![]() ;
;
(3)如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PAPB=kAB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
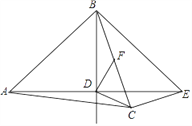
(1)若BD=DE=![]() ,CE=
,CE=![]() ,求BC的长;
,求BC的长;
(2)若BD=DE,求证:BF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD 中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N ,连接OM,ON,MN .下列五个结论:①△CNB≌△DMC ;②△CON≌△DOM ;③△OMN≌△OAD ;④![]() ;⑤若AB=2,则
;⑤若AB=2,则![]() 的最小值是
的最小值是![]() ,其中正确结论的个数是 ( )
,其中正确结论的个数是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com