
����Ŀ��Ŀǰ������У�ֻ�������Խ��Խ�ܵ�����ע�����������������ij��ѧ���꼶��ѧ��ȤС���ͬѧ���������ѧУ�������ҳ�������ѧ�����ֻ�������Ŀ�����ͳ�����������������µ�ͳ��ͼ��
��1����ε���ļҳ�����Ϊ________�ˣ��ҳ���ʾ������ͬ��������Ϊ________����
��2������ͼ���а�����ͳ��ͼ����������
��3������ν��ܵ���ļҳ���������һ����ǡ��������ͬ���ļҳ��ĸ�����________��
��4����ͼ���б�ʾ�ҳ�������ν��������Բ�ĽǵĶ�����

���𰸡���1��600��80��2��120�ˣ���ͼ����������3��60����4��24��.
�������������������1�������ɵ���������ռ�İٷֱ���ʽ���㼴�������ļҳ���������Ȼ��������ɵ�������
��2����������������ռ�ٷֱȵõ�����������ͼ�μ�����
��3����������ͳ��ͼ���ɵõ�ǡ���ǡ���ͬ���ļҳ��ĸ�����
��4���������ν��������ռ�İٷֱ����ٳ���360�㣬���㼴�ɵý⣮
���������������1������ļҳ�����Ϊ��360��60%=600��������ͬ��������600��20%=120��������ͬ��������600��120��360��40=80����
��2��600��20%=120������ͼ����ͼ��

��3������ͬ��̬�ȵļҳ��ĸ�����60%��
��4����ʾ�ҳ�������ν����Բ�ĽǵĶ���Ϊ�� ![]() ��360��=24����
��360��=24����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ADE+��BCF=180����BEƽ�֡�ABC����ABC=2��E.
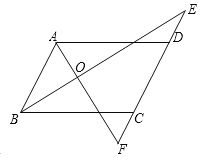
��1��AD��BCƽ������˵�����ɣ�
��2��AB��EF��λ�ù�ϵ��Σ�Ϊʲô��
��3����AFƽ�֡�BAD����˵����
�١�BAD=2��F���ڡ�E+��F=90��.
ע������ڣ�1������2��С��������Ľ����̵Ŀո�����д���ɻ���ѧʽ���ڣ�3��С��Ҫд���������.
�⣺��1��AD��BC���������£�
�ߡ�ADE+��ADF=180������ƽ�ǵĶ��壩
��ADE+��BCF=180��������֪��
���ADF=��______�� ��____________________________��
�� AD��BC ��____________________________��
��2��AB��EF��λ�ù�ϵ�ǣ�_______________.
��BEƽ�֡�ABC�� ����֪��
���ABE=![]() ��ABC. ����ƽ���ߵĶ��壩
��ABC. ����ƽ���ߵĶ��壩
�֡ߡ�ABC=2��E, ����֪����
����E=![]() ��ABC,
��ABC,
���E=��_____. ��_____________________________��
�� ______��_____. ��_____________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�����![]() ��
��![]() �ֱ���
�ֱ���![]() ��Ĵ��ߣ�����ֱ�Ϊ
��Ĵ��ߣ�����ֱ�Ϊ![]() ��
��![]() ��
��
(1)��ֱ��![]() ��ֱ��
��ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
(2)��![]() Ϊֱ��
Ϊֱ��![]() �ϵ�һ�����㣬��
�ϵ�һ�����㣬��![]() ��
��![]() ��Ĵ��߽�ֱ��
��Ĵ��߽�ֱ��![]() �ڵ�
�ڵ�![]() ���Ƿ���������ĵ�
���Ƿ���������ĵ�![]() ��ʹ����
��ʹ����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı���Ϊƽ���ı��Σ������ڣ����ʱ��
Ϊ������ı���Ϊƽ���ı��Σ������ڣ����ʱ��![]() �ĺ����ꣻ�������ڣ���˵�����ɣ�
�ĺ����ꣻ�������ڣ���˵�����ɣ�
(3)��![]() ��
��![]() ����ƽ��(��
����ƽ��(��![]() ���߶�
���߶�![]() �ϣ��Ҳ����
�ϣ��Ҳ����![]() �غ�)����ƽ�ƵĹ����У���ƽ�ƾ���Ϊ
�غ�)����ƽ�ƵĹ����У���ƽ�ƾ���Ϊ![]() ��
��![]() ��
��![]() �ص����ֵ������Ϊ
�ص����ֵ������Ϊ![]() ������
������![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��5![]() ��3
��3![]() ��4
��4![]() ��
��![]()
��2����![]() ��
��![]() ��
��![]() ��������36��
��������36��
��3����![]() �D(1�D0.5)��
�D(1�D0.5)��![]() ��[2��(��4)2]
��[2��(��4)2]
��4����![]() ��
��![]() ����52��|��
����52��|��![]() |����
|����![]() ��2019��42020
��2019��42020
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ���߶�
���߶�![]() .
.
��1����ͼ������![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ��
��![]() ����
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬���߶�
���е㣬���߶�![]() �ij����� ��
�ij����� ��
![]()
��2�����ѣ�1���е�![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ��
��![]() ������
����Ϊ��![]() ���߶�
���߶�![]() ������һ�㣬��
������һ�㣬��![]() ��
��![]() �������������䣬������߶�
�������������䣬������߶�![]() �ij��ȣ��ú�
�ij��ȣ��ú�![]() ��
��![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��3�����ѣ�2���е�![]() ���߶�
���߶�![]() ������һ�㣬��Ϊ��
������һ�㣬��Ϊ��![]() ��ֱ��
��ֱ��![]() ������һ�㣬�����������䣬���߶�
������һ�㣬�����������䣬���߶�![]() �ij��Ȼ�仯�����б仯��������.
�ij��Ȼ�仯�����б仯��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
��![]() ��0����
��0����![]() ���ϵ�һ�����㣬����ԭ��ľ����2��Ϊ
���ϵ�һ�����㣬����ԭ��ľ����2��Ϊ![]() .
.
��1����![]() ����
����![]() �ĺ�������ʽ���������������л����������ͼ��
�ĺ�������ʽ���������������л����������ͼ��
��2��������������![]() ��
��![]() ��ͼ���뺯��
��ͼ���뺯��![]() ��ͼ���ཻ�ڵ�
��ͼ���ཻ�ڵ�![]() ���ҵ�
���ҵ�![]() ��������Ϊ2.
��������Ϊ2.
����k��ֵ��
�ڽ��ͼ��![]() ��
��![]() ʱ��д��
ʱ��д��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��3����ԭ���һ��ֱ�߽�![]() ��
��![]() ��
��![]() ��0����
��0����![]() ��
��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ���Ҳࣩ���ֱ����
���Ҳࣩ���ֱ����![]() ��
��![]() ��
��![]() ���
���![]() ���ƽ���ߣ���ƽ���߽��ڵ�
���ƽ���ߣ���ƽ���߽��ڵ�![]() �����
�����![]() ������� .
������� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AD//BC��AD=AB=2����B=120�㣬��ADC=150�������ԶԽ���ACΪ�����Dһ�����ȱ���ACE�����ı���ABCE�����=______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
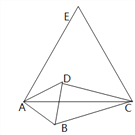
����Ŀ����ͼ����֪��ABC�ǵȱ�������,��D��ֱ��BC��һ��,��ADΪһ����AD���Ҳ����ȱߡ�ADE.���DCE�Ĵ�С.
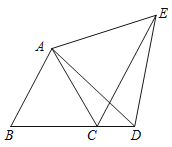
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ����������������ȷ���ǣ�������

A. ��O����ֱ��AC��
B. ����AB������BC��ָͬһ������
C. ͼ�й���5���߶�
D. ֱ��AB��ֱ��CA��ָͬһ��ֱ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com