练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知如图，则下列叙述不正确的是（　　）

    A. 点O不在直线AC上

    B. 射线AB与射线BC是指同一条射线

    C. 图中共有5条线段

    D. 直线AB与直线CA是指同一条直线

    【答案】B

    【解析】

    根据点与直线的关系可知点O不在直线AC上，故A说法正确，不符合题意；

    射线表示方法是端点字母在前，故B错误，符合题意；

    图中有线段AB、AC、BC、OB、OC，共5条，故C说法正确，不符合题意；

    直线表示方法是用直线上两个点表示，没有先后顺序，故D正确，不符合题意．

    A、点O不在直线AC上，故A说法正确，不符合题意；

    B、射线AB与射线BC不是指同一条射线，故B错误，符合题意；

    C、图中有线段AB、AC、BC、OB、OC，共5条，故C说法正确，不符合题意；

    D、直线AB与直线CA是指同一条直线，故D正确，不符合题意．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，过点A作AG⊥EB，垂足为G，AG交BD于F，则OE=OF．

    （1）请证明0E=OF

    （2）解答（1）题后，某同学产生了如下猜测：对上述命题，若点E在AC的延长线上，AG⊥EB，AG交 EB的延长线于 G，AG的延长线交DB的延长线于点F，其他条件不变，则仍有OE=OF．问：猜测所得结论是否成立？若成立，请给出证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边△A1C1C2的周长为1，作C1D1⊥A1C2于D1，在C1C2的延长线上取点C3，使D1C3=D1C1，连接D1C3，以C2C3为边作等边△A2C2C3；作C2D2⊥A2C3于D2，在C2C3的延长线上取点C4，使D2C4=D2C2，连接D2C4，以C3C4为边作等边△A3C3C4；…且点A1，A2，A3，…都在直线C1C2同侧，如此下去，则△A1C1C2，△A2C2C3，△A3C3C4，…，△AnCnCn+1的周长和为______．（n≥2，且n为整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，已知点A（﹣3，0）、B（0，4），对△OAB连续作旋转变换，依次得到△1、△2、△3、△4…，则△2016的直角坐标顶点的坐标为（ ）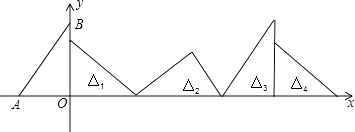

    A.（8053，0）
    B.（8064，0）
    C.（8053， ）
    D.（8064， ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学为了响应国家发展足球的战略方针，激发学生对足球的兴趣，特举办全员参与的“足球比赛”，赛后，全校随机抽查部分学生，其成绩（百分制）整理分成5组，并制成如下频数分布表和扇形统计图，请根据所提供的信息解答下列问题：
    成绩频数分布表

    组别

    成绩（分）

    频数

    A

    50≤x＜60

    6

    B

    60≤x＜70

    m

    C

    70≤x＜80

    20

    D

    80≤x＜90

    36

    E

    90≤x＜100

    n


    （1）频数分布表中的m= ， n=；
    （2）样本中位数所在成绩的级别是 ， 扇形统计图中，E组所对应的扇形圆心角的度数是；
    （3）若该校共有2000名学生，请你估计体育综合测试成绩不少于80分的大约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料： 如图1，在平面直角坐标系xOy中，直线y1=ax+b与双曲线y2= 交于A（1，3）和B（﹣3，﹣1）两点．

    观察图象可知：
    ①当x=﹣3或1时，y1=y2；
    ②当﹣3＜x＜0或x＞1时，y1＞y2 ， 即通过观察函数的图象，可以得到不等式ax+b＞ 的解集．
    有这样一个问题：求不等式x3+4x2﹣x﹣4＞0的解集．
    某同学根据学习以上知识的经验，对求不等式x3+4x2﹣x﹣4＞0的解集进行了探究．
    下面是他的探究过程，请将（1）、（2）、（3）补充完整：
    将不等式按条件进行转化：
    当x=0时，原不等式不成立；
    当x＞0时，原不等式可以转化为x2+4x﹣1＞ ；
    当x＜0时，原不等式可以转化为x2+4x﹣1＜ ；
    （1）构造函数，画出图象 设y3=x2+4x﹣1，y4= ，在同一坐标系中分别画出这两个函数的图象．
    双曲线y4= 如图2所示，请在此坐标系中画出抛物线y3=x2+4x﹣1；（不用列表）

    （2）确定两个函数图象公共点的横坐标 观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足y3=y4的所有x的值为；
    （3）借助图象，写出解集 结合讨论结果，观察两个函数的图象可知：不等式x3+4x2﹣x﹣4＞0的解集为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）直线y=kx+4经过点（1，2），求不等式kx+4≥0的解集．

    （2）x取哪些正整数时，不等式 x+3>6 与 2x-1<10 都成立？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    (1)2－7＋5－3;

    (2)－－＋－；

    (3)(－40)－(＋27)＋19－24－(－32)；

    (4)0.5－＋－－；

    (5)|－3.5|－ ＋

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n+0.5，n为整数），例如：[2.3]=2，（2.3）=3，[2.3）=2．当﹣1＜x＜1时，化简 [x]+（x）+[x）的结果是__________________．

    查看答案和解析>>

    同步练习册答案