
【题目】点![]() (
(![]() ,0)是
,0)是![]() 轴上的一个动点,它与原点的距离的2倍为
轴上的一个动点,它与原点的距离的2倍为![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并在所给网格中画出这个函数图象;
的函数解析式,并在所给网格中画出这个函数图象;
(2)若反比例函数![]() =
=![]() 的图象与函数
的图象与函数![]() 的图象相交于点
的图象相交于点![]() ,且点
,且点![]() 的纵坐标为2.
的纵坐标为2.
①求k的值;
②结合图象,当![]() >
>![]() 时,写出
时,写出![]() 的取值范围.
的取值范围.
(3)过原点的一条直线交![]() =
=![]() (
(![]() >0)于
>0)于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),分别过点
的右侧),分别过点![]() 、
、![]() 作
作![]() 轴和
轴和![]() 轴的平行线,两平行线交于点
轴的平行线,两平行线交于点![]() ,则△
,则△![]() 的面积是 .
的面积是 .
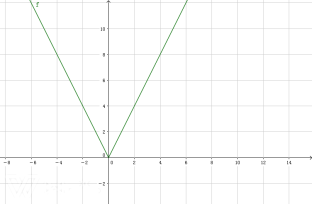
【答案】(1)y1=2丨x丨,图像见解析;(2)①当P点坐标为P1(-1,2)时,k=-2;当P点坐标为P2(1,2)时,k=2,②当P点坐标为P1(-1,2)时,x<-1或x>0;当P点坐标为P2(1,2)时, x<0或者x>1(3)4
【解析】
(1)由OM的长度的2倍可直接得到y1函数解析式 (2)因为y1的函数图像分段了,所以对P的考虑要分情况,然后根据分的情况按照图像进行解题即可 (3)得到K的值之后按照k的几何意义解题即可
(1)OM的长为丨x丨,则y1=2丨x丨,图像如下图所示
(2)P点纵坐标为2,所以P点有两种情况,P1(-1,2),P2(1,2)
1°当P点坐标为P1(-1,2)时,k=-2,图像如下图
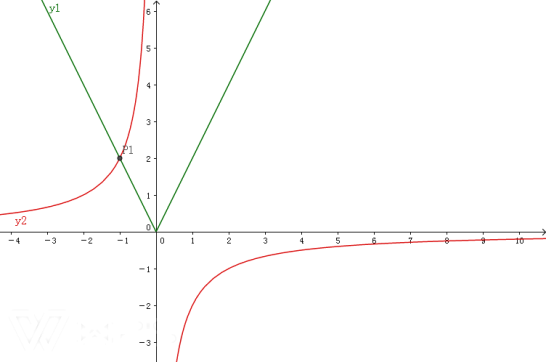
由图像得![]() >
>![]() 时,x<-1或x>0
时,x<-1或x>0
2°当P点坐标为P2(1,2)时,k=2,图像如下图
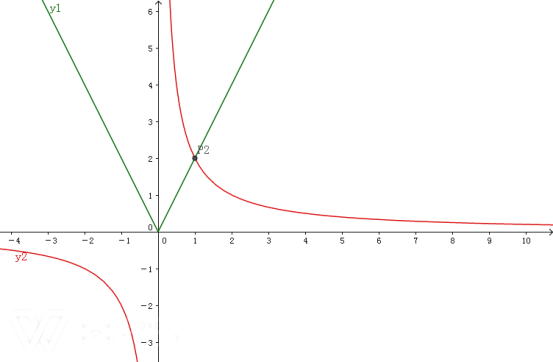
由图像可知,当![]() >
>![]() 时,x<0或者x>1
时,x<0或者x>1
(3)k>0,且由(2)可得,k=2,图像如下图
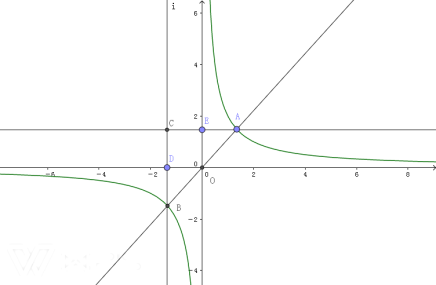
由反比例函数k的几何意义可得![]() ,矩形ODCE的面积为2
,矩形ODCE的面积为2
所以△![]() 的面积是1+1+2=4
的面积是1+1+2=4


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F分别是AD,BC的中点,连结AF,BE,CE,DF分别交于点M,N,则四边形EMFN是( )

A. 梯形B. 菱形
C. 矩形D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数![]() =
=![]() 与反比例函数
与反比例函数![]() =
=![]() 的图像有一个交点
的图像有一个交点![]() (
(![]() ,3),
,3),![]() ⊥
⊥![]() 轴于点
轴于点![]() ,平移直线
,平移直线![]() =
=![]() ,使其经过点
,使其经过点![]() ,得到直线
,得到直线![]() ,则直线
,则直线![]() 对应的函数解析式是_____________.
对应的函数解析式是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,双曲线
中,双曲线![]() =
=![]() 经过□
经过□![]() 的顶点
的顶点![]() 、
、![]() ,点
,点![]() 的坐标为(
的坐标为(![]() ,
,![]() 1),点
1),点![]() 在
在![]() 轴上,且
轴上,且![]() ∥
∥![]() 轴,平行四边形
轴,平行四边形![]() 的面积是8.
的面积是8.
(1)求双曲线和AB所在直线的解析式;
(2)点![]() (
(![]() ,
,![]() )、
)、![]() (
(![]() ,
,![]() )是双曲线
)是双曲线![]() =
=![]() (
(![]() <0)图象上的两点,若
<0)图象上的两点,若![]() >
>![]() ,则
,则![]()
![]() ;(填“<”、“=”或“>”)
;(填“<”、“=”或“>”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前我市“校园手机”现象越来越受到社会关注,针对这种现象,我市某中学九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的看法,统计整理并制作了如下的统计图:
(1)这次调查的家长总数为________人.家长表示“不赞同”的人数为________人;
(2)请在图①中把条形统计图补充完整;
(3)从这次接受调查的家长中随机抽查一个,恰好是“赞同”的家长的概率是________;
(4)求图②中表示家长“无所谓”的扇形圆心角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
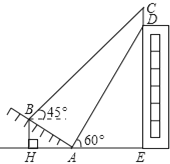
【题目】如图,我市某中学在创建“特色校园”的活动中,将学校的办学理念做成了宣传牌(CD),放置在教学楼的顶部(如图所示),该中学数学活动小组的同学在山坡坡脚A处测得宣传牌底D的仰角为60°,沿坡AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求宣传牌CD的高度.(结果精确到0.1米.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
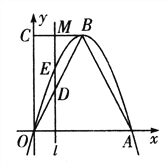
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于O点、A点,B为抛物线上一点,C为y轴上一点,连接BC,且BC//OA,已知点O(0,0),A(6,0),B(3,m),AB=
轴交于O点、A点,B为抛物线上一点,C为y轴上一点,连接BC,且BC//OA,已知点O(0,0),A(6,0),B(3,m),AB=![]() .
.
(1)求B点坐标及抛物线的解析式.,
(2)M是CB上一点,过点M作y轴的平行线交抛物线于点E,求DE的最大值;
(3)坐标平面内是否存在一点F,使得以C、B、D、F为顶点的四边形是菱形?若存在,求出符合条件的点F坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E,F分别是□ABCD的边BC,AD上的中点,且∠BAC=90°.
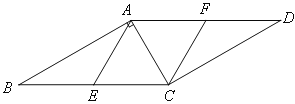
(1)求证:四边形AECF是菱形;
(2)若∠B=30°,BC=10,求菱形AECF面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com