
【题目】如图,在矩形ABCD中,E,F分别是AD,BC的中点,连结AF,BE,CE,DF分别交于点M,N,则四边形EMFN是( )

A. 梯形B. 菱形
C. 矩形D. 无法确定
【答案】B
【解析】
求出四边形ABFE为平行四边形,四边形BFDE为平行四边形,根据平行四边形的性质得出BE∥FD,即ME∥FN,同理可证EN∥MF,得出四边形EMFN为平行四边形,求出ME=MF,根据菱形的判定得出即可.
连接EF.
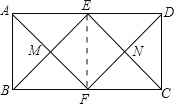
∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
又∵E,F分别为AD,BC中点,
∴AE∥BF,AE=BF,ED∥CF,DE=CF,
∴四边形ABFE为平行四边形,四边形BFDE为平行四边形,
∴BE∥FD,即ME∥FN,
同理可证EN∥MF,
∴四边形EMFN为平行四边形,
∵四边形ABFE为平行四边形,∠ABC为直角,
∴ABFE为矩形,
∴AF,BE互相平分于M点,
∴ME=MF,
∴四边形EMFN为菱形.
故选B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,反比例函数y=![]() 的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
(1)求反比例函数与一次函数的解析式及B点坐标;
(2)若C是y轴上的点,且满足△ABC的面积为10,求C点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的有( )
①有理数包括正有理数和负有理数; ②绝对值等于它本身的数是非负数;③若|b|=|﹣5|,则b=-5 ; ④当b=2时,5﹣|2b﹣4|有最小值是5;⑤若![]() 、
、![]() 互为相反数,则
互为相反数,则![]() ;⑥
;⑥![]() 是关于
是关于![]() 、
、![]() 的六次三项式.
的六次三项式.
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=12,AB=10,则AE的长为( )

A. 16B. 15C. 14D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
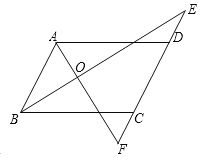
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:
①∠BAD=2∠F;②∠E+∠F=90°.
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:(1)AD∥BC,理由如下:
∵∠ADE+∠ADF=180°,(平角的定义)
∠ADE+∠BCF=180°,(已知)
∴∠ADF=∠______, (____________________________)
∴ AD∥BC (____________________________)
(2)AB与EF的位置关系是:_______________.
∵BE平分∠ABC, (已知)
∴∠ABE=![]() ∠ABC. (角平分线的定义)
∠ABC. (角平分线的定义)
又∵∠ABC=2∠E, (已知),
即∠E=![]() ∠ABC,
∠ABC,
∴∠E=∠_____. (_____________________________)
∴ ______∥_____. (_____________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
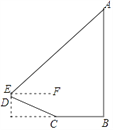
A. 22.5 米 B. 24.0 米 C. 28.0 米 D. 33.3 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】松雷中学图书馆近日购进甲、乙两种图书,每本甲图书的进价比每本乙图书的进价高20元,花780元购进甲图书的数量与花540元购进乙图书的数量相同.
(1)求甲、乙两种图书每本的进价分别是多少元?
(2)松雷中学计划购进甲、乙两种图书共70本,总购书费用不超过4000元,则最多购进甲种图书多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织全校1500名师生外出参加集体活动.经过研究,决定租用当地租车公司一共60辆![]() 、
、![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 400元 |
| 20人 | 300元 |
注:载客量指的是每辆客车最多可载该校师生的人数.
学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过22000元,一共有几种租车方案?并结合函数性质说明哪种租车方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() (
(![]() ,0)是
,0)是![]() 轴上的一个动点,它与原点的距离的2倍为
轴上的一个动点,它与原点的距离的2倍为![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并在所给网格中画出这个函数图象;
的函数解析式,并在所给网格中画出这个函数图象;
(2)若反比例函数![]() =
=![]() 的图象与函数
的图象与函数![]() 的图象相交于点
的图象相交于点![]() ,且点
,且点![]() 的纵坐标为2.
的纵坐标为2.
①求k的值;
②结合图象,当![]() >
>![]() 时,写出
时,写出![]() 的取值范围.
的取值范围.
(3)过原点的一条直线交![]() =
=![]() (
(![]() >0)于
>0)于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),分别过点
的右侧),分别过点![]() 、
、![]() 作
作![]() 轴和
轴和![]() 轴的平行线,两平行线交于点
轴的平行线,两平行线交于点![]() ,则△
,则△![]() 的面积是 .
的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com