
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣mx+n.
(1)当m=2时,
①求抛物线的对称轴,并用含n的式子表示顶点的纵坐标;
②若点A(﹣2,y1),B(x2,y2)都在抛物线上,且y2>y1,则x2的取值范围是 ;
(2)已知点P(﹣1,2),将点P向右平移4个单位长度,得到点Q.当n=3时,若抛物线与线段PQ恰有一个公共点,结合函数图象,求m的取值范围.
【答案】(1)①n﹣1;②x2<﹣2或x2>4;(2)m≤﹣2或m=2或![]() .
.
【解析】
(1)①把m=2代入抛物线解析式,利用x=![]() ,求出对称轴,然后把顶点横坐标代入,即可用含n的式子表示出顶点的纵坐标;
,求出对称轴,然后把顶点横坐标代入,即可用含n的式子表示出顶点的纵坐标;
②利用抛物线的对称性,及开口向上,可知离对称轴越远,函数值越大,从而可解;
(2)把n=3代入,再分抛物线经过点Q,抛物线经过点P(1,2),抛物线的顶点在线段PQ上,三种情况分类讨论,得出相应的m值,从而得结论.
解:(1)①∵m=2,
∴抛物线为y=x2﹣2x+n.
∵x![]() 1,
1,
∴抛物线的对称轴为直线x=1.
∵当线x=1时,y=1﹣2+n=n﹣1,
∴顶点的纵坐标为:n﹣1.
②∵抛物线的对称轴为直线x=1,开口向上,
x=﹣2到x=1的距离为3,
∴点A(﹣2,y1),B(x2,y2)都在抛物线上,且y2>y1,则x2的取值范围是x2<﹣2或x2>4,
故答案为:x2<﹣2或x2>4.
(2)∵点P(﹣1,2),向右平移4个单位长度,得到点Q.
∴点Q的坐标为(3,2),
∵n=3,
抛物线为y=x2﹣mx+3.
当抛物线经过点Q(3,2)时,2=32﹣3m+3,解得![]() ;
;

当抛物线经过点P(﹣1,2)时,2=(﹣1)2+m+3,解得m=﹣2;
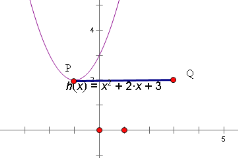
当抛物线的顶点在线段PQ上时,![]() 2,解得m=±2.
2,解得m=±2.
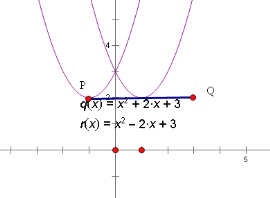
结合图象可知,m的取值范围是m≤﹣2或m=2或![]() .
.
故答案为:m≤﹣2或m=2或![]() .
.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象过点P(﹣![]() ,0),且与反比例函数
,0),且与反比例函数![]() (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.
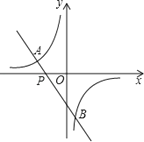
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
查看答案和解析>>
科目:初中数学 来源: 题型:
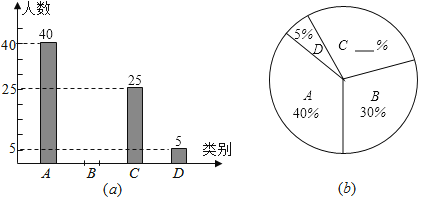
【题目】为了了解某区2018年初中毕业生毕业后的去向,某区教育部门对部分初三学生进行了抽样调查,就初三学生的四种去向(A,读普通高中;B,读职业高中;C,直接进入社会就业;D,其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请问:
(1)此次共调查了多少名初中毕业生?
(2)将两幅统计图中不完整的部分补充完整;
(3)若某区2018年初三毕业生共有3500人,请估计2019年初三毕业生中读普通高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地出发沿一条笔直的公路骑行前往乙地,她与乙地之间的距离y(km)与出发时间t(h)之间的函数关系如图中线段AB所示,在小丽出发的同时,小明从乙地沿同一条公路汽骑车匀速前往甲地,两人之间的距离s(km)与出发时间t(h)之间的函数关系如图中折线段AD-DE-EF所示,则E点坐标为
________.

查看答案和解析>>
科目:初中数学 来源: 题型:
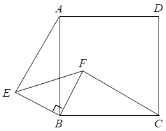
【题目】如图,△EBF为等腰直角三角形,点B为直角顶点, 四边形ABCD是正方形.
⑴ 求证:△ABE≌△CBF;
⑵ CF与AE有什么特殊的位置关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
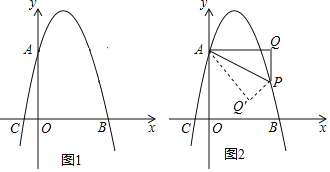
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,试过点P作x轴的垂线1,再过点A作1的垂线,垂足为Q,连接AP.
(1)求抛物线的函数表达式和点C的坐标;
(2)若△AQP∽△AOC,求点P的横坐标;
(3)如图2,当点P位于抛物线的对称轴的右侧时,若将△APQ沿AP对折,点Q的对应点为点Q′,请直接写出当点Q′落在坐标轴上时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E是矩形ABCD的边BC上一点,EF⊥AE,分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.
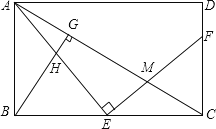
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=4,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
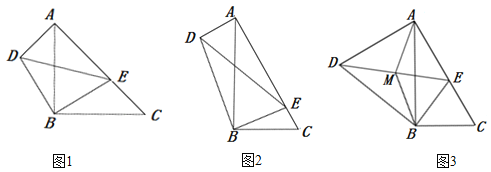
如图1,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=45°,点E是线段AC上一动点,连接DE.
填空:①则![]() 的值为______;②∠EAD的度数为_______.
的值为______;②∠EAD的度数为_______.
(2)类比探究
如图2,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=60°,点E是线段AC上一动点,连接DE.请求出![]() 的值及∠EAD的度数;
的值及∠EAD的度数;
(3)拓展延伸
如图3,在(2)的条件下,取线段DE的中点M,连接AM、BM,若BC=4,则当△ABM是直角三角形时,求线段AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com