
 如图,一次函数y=-x-1与反比例函数y=$\frac{m}{x}$在第二象限交于点A,一次函数y=-x-1与坐标轴分别交于B、C两点,连结AO,若tan∠AOB=$\frac{1}{3}$.
如图,一次函数y=-x-1与反比例函数y=$\frac{m}{x}$在第二象限交于点A,一次函数y=-x-1与坐标轴分别交于B、C两点,连结AO,若tan∠AOB=$\frac{1}{3}$.分析 (1)设出A点的坐标为(a,b)(a<0),结合题意,由于tan∠AOB=$\frac{1}{3}$,易得出3b+a=0;又因为A点一次函数图象上,即有-a-1=b,两方程联立即可得出A点的坐标,代入反比例函数解析式中,得k,便可得出反比例函数解析式;
(2)利用一次函数解析式,得出C点的坐标,易得OC的长,结合(1),可得出点A到y轴的距离为A点横坐标的绝对值,代入三角形面积公式,即可得出△AOC的面积.然后设出D的坐标,根据三角形的面积公式求解.
解答 解:(1)设A(a,b),结合题意,
-a-1=b,
又tan∠AOB=$\frac{1}{3}$,
即有3b+a=0;
可得出a=$\frac{3}{2}$,b=$\frac{1}{2}$;
即A($\frac{3}{2}$,$\frac{1}{2}$),
代入反比例函数解析式中,有$\frac{1}{2}$=$\frac{m}{-\frac{3}{2}}$,
得m=$\frac{3}{4}$,
故反比例函数解析式为:y=$\frac{3}{4x}$;
(2)因为一次函数y=-x-1与坐标轴交C点,
令x=0,得y=-1,
即C(0,-1);
所以OC=1;
又∵A(-$\frac{3}{2}$,$\frac{1}{2}$),
即点A到x轴的距离为$\frac{1}{2}$,
因为一次函数y=-x-1与x轴交B点,
令y=0,得x=-1,
即B(-1,0);
则OB=1,
所以S△AOC=$\frac{1}{2}$OB•$\frac{1}{2}$+$\frac{1}{2}$OB•OC=$\frac{3}{4}$.
设D的横坐标是(m,0),
则BD=|m+1|.
则$\frac{1}{2}$|m+1|×1=$\frac{3}{4}$,
解得:m=$\frac{1}{2}$或-$\frac{5}{2}$.
则D的坐标是($\frac{1}{2}$,0)或(-$\frac{5}{2}$,0).
点评 本题主要考查了反比例函数和一次函数的综合应用,以及三角形的面积的求法等知识点,题目较为简单,适合学生平时的练习使用.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
| 月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
| 钱数变化 | +300 | +220 | -150 | -100 | +330 | +200 | +280 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
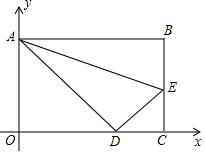 如图,在矩形OABC中,点C在x轴上,点A在y轴上,且OA,OC的长分别是一元二次方程x2-18x+80=0的两个根(OA<OC),点E在BC上,将△ABE沿AE折叠,使点B落在OC上.
如图,在矩形OABC中,点C在x轴上,点A在y轴上,且OA,OC的长分别是一元二次方程x2-18x+80=0的两个根(OA<OC),点E在BC上,将△ABE沿AE折叠,使点B落在OC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y=-x2+2x+m图象过点A(3,0),与y轴交于点B
如图,已知二次函数y=-x2+2x+m图象过点A(3,0),与y轴交于点B查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com