
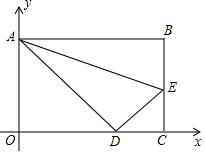
 ��ͼ���ھ���OABC�У���C��x���ϣ���A��y���ϣ���OA��OC�ij��ֱ���һԪ���η���x2-18x+80=0����������OA��OC������E��BC�ϣ�����ABE��AE�۵���ʹ��B����OC�ϣ�
��ͼ���ھ���OABC�У���C��x���ϣ���A��y���ϣ���OA��OC�ij��ֱ���һԪ���η���x2-18x+80=0����������OA��OC������E��BC�ϣ�����ABE��AE�۵���ʹ��B����OC�ϣ����� ��1����һԪ���η��̿����OA��OC�ij��������õ�A��C�����ꣻ
��2�����۵������ʿɵ�AD=AB��DE=BE����Rt��AOD�п����OD��������CD����CE=y�������y��ʾ��DE�ij�����Rt��CDE�У��ɹ��ɶ����ɵõ�����y�ķ��̣������CE�ij���������E�����꣬���뷴������������ʽ�����k��ֵ��
��3���ô���ϵ���������ֱ��AD��DE�Ľ���ʽ����������M�ĺ�����Ϊt����CDΪƽ���ı��εı�ʱ������t�ɱ�ʾ��MN����MN=CD�ɵõ�����t�ķ��̣������t��ֵ�������M������ꣻ��CDΪ�Խ���ʱ����ͼ4����M��MG��OC��G����֪��ʱƽ���ı���Ϊ���Σ�����ͬ�ǵ����Ǻ������MG��CG�ij����Ӷ��ɵõ�M�����꣮
���  �⣺��1���ⷽ��x2-18x+80=0���ɵ�x=10��x=8��
�⣺��1���ⷽ��x2-18x+80=0���ɵ�x=10��x=8��
��OA��OC�ij��ֱ���һԪ���η���x2-18x+80=0����������OA��OC����
��OA=8��OC=10��
��A��0��8����C��10��0����
��2�����۵��ã�AD=AB=10��DE=BE��
��Rt��AOD�У��ɹ��ɶ����ɵã�OD=$\sqrt{A{D}^{2}-O{A}^{2}}$=6��
��CD=OC-OD=10-6=4��
��CE=y����BE=DE=8-y��
��Rt��CDE�У��ɹ��ɶ����ɵã�DE2=CE2+DC2��
����8-y��2=y2+42�����y=3��
��E��10��3����
�߷���������y=$\frac{k}{x}$��ͼ����E��
��k=10��3=30��
��3����A��0��8����D��6��0����E��10��3����
����ֱ��AD����ʽΪy=kx+8��
��D��6��0����A��0��8������ɵã�$\left\{\begin{array}{l}{6k+b=0}\\{b=8}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=8}\end{array}\right.$��
��ֱ��AD����ʽΪy=-$\frac{4}{3}$x+8��
��ֱ��DE����ʽΪy=mx+s��
��D��E�������ɵ�$\left\{\begin{array}{l}{6m+s=0}\\{10m+s=3}\end{array}\right.$�����$\left\{\begin{array}{l}{m=\frac{3}{4}}\\{s=-\frac{9}{2}}\end{array}\right.$��
��ֱ��DE����ʽΪy=$\frac{3}{4}$x-$\frac{9}{2}$��
�ߵ�M��ֱ��AD�ϣ�
����M��t��-$\frac{4}{3}$t+8����
����C��D��M��NΪ������ı�����ƽ���ı��Σ�
����CDΪ�ߺ�CDΪ�Խ������������
�ٵ�CDΪ��ʱ����MN��CD����MN=CD=4��
��M��N��x���Ϸ�ʱ����ͼ2����N������Ϊ��t+4��-$\frac{4}{3}$t+8����
����ֱ��DE����ʽ�ɵ�-$\frac{4}{3}$t+8=$\frac{3}{4}$��t+4��-$\frac{9}{2}$�����t=$\frac{114}{25}$
��t=$\frac{114}{25}$ʱ��-$\frac{4}{3}$t+8=-$\frac{4}{3}$��$\frac{114}{25}$+8=$\frac{48}{25}$
��M��$\frac{114}{25}$��$\frac{48}{25}$����
��M��N��x���·�ʱ����N������Ϊ��t-4��-$\frac{4}{3}$t+8����
����ֱ��DE����ʽ�ɵ�-$\frac{4}{3}$t+8=$\frac{3}{4}$��t-4��-$\frac{9}{2}$�����t=$\frac{186}{25}$
��t=$\frac{186}{25}$ʱ��-$\frac{4}{3}$t+8=-$\frac{4}{3}$��$\frac{186}{25}$+8=-$\frac{48}{25}$
��M��$\frac{186}{25}$��-$\frac{48}{25}$����
�ڵ�CDΪ�Խ���ʱ����ͼ4����M��MG��OC��G��
���۵��ã���ADE=��B=90�㣬
���EDM=90�㣬
��?DMCN�Ǿ��Σ�
���DNC=��DMC=90�㣬
sin��EDC=$\frac{EC}{ED}=\frac{NC}{DC}$��
��$\frac{3}{5}=\frac{NC}{4}$��
��NC=$\frac{12}{5}$��
�ɹ��ɶ����ã�DN=$\sqrt{{4}^{2}-��\frac{12}{5}��^{2}}$=$\frac{16}{5}$��
��DM=NC=$\frac{12}{5}$��CM=DN=$\frac{16}{5}$��
��DN��MC��
���EDC=��DCM��
sin��EDC=sin��DCM=$\frac{3}{5}$=$\frac{MG}{CM}$��
$\frac{3}{5}$=$\frac{MG}{\frac{16}{5}}$��
��MG=$\frac{48}{25}$��
ͬ���ɵã�CG=$\frac{64}{25}$��
��OG=10-$\frac{64}{25}$=$\frac{186}{25}$��
��M��$\frac{186}{25}$��-$\frac{48}{25}$����
�������������ڵ�M�͵�N��ʹ��C��D��M��NΪ������ı�����ƽ���ı��Σ���M������Ϊ��$\frac{114}{25}$��$\frac{48}{25}$����$\frac{186}{25}$��-$\frac{48}{25}$����
���� �����Ƿ��������������Ρ����̵��ۺ��⣬������������ͼ���ص㣬���Ρ�ƽ���ı��ε����ʣ����Ǻ��������ɶ������۵���֪ʶ���ۺ��Խ�ǿ���Ѷ����У�ע��������д��ڵ�ƽ���ı���Ҫ���÷������۵�˼�룬��Ҫ©�⣬Ҫ��CDΪ�ߺͶԽ��������濼�ǣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У��ȱߡ�ABC�Ķ���B��C������ֱ�Ϊ��2��0������6��0������N��A�������AC��C���˶�������ON��AB�ڵ�M������Mǡƽ���߶�ONʱ�����߶�CN�ij���
��ͼ����ƽ��ֱ������ϵ�У��ȱߡ�ABC�Ķ���B��C������ֱ�Ϊ��2��0������6��0������N��A�������AC��C���˶�������ON��AB�ڵ�M������Mǡƽ���߶�ONʱ�����߶�CN�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��1�����ʵ��ķ���������һԪ���η��̣�x2-6x+1=0��
��1�����ʵ��ķ���������һԪ���η��̣�x2-6x+1=0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ�κ���y=-x-1�뷴��������y=$\frac{m}{x}$�ڵڶ������ڵ�A��һ�κ���y=-x-1��������ֱ���B��C���㣬����AO����tan��AOB=$\frac{1}{3}$��
��ͼ��һ�κ���y=-x-1�뷴��������y=$\frac{m}{x}$�ڵڶ������ڵ�A��һ�κ���y=-x-1��������ֱ���B��C���㣬����AO����tan��AOB=$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com