
【题目】如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数. 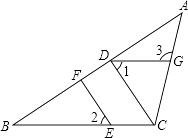
【答案】
(1)解:CD平行于EF,
理由是:∵CD⊥AB,EF⊥AB,
∴∠CDF=∠EFB=90°,
∴CD∥EF;
(2)解:∵CD∥EF,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴BC∥DG,
∴∠3=∠ACB,
∵∠3=115°,
∴∠ACB=115°.
【解析】(1)根据垂直定义求出∠CDF=∠EFB=90°,根据平行线的判定推出即可;(2)根据平行线的性质得出∠2=∠DCB,求出∠1=∠DCB,根据平行线的判定得出BC∥DG,根据平行线的性质得出∠3=∠ACB即可.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】(枣庄)
已知:在直角坐标平面内,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长是一个单位长度)
(1) 在备用图(1)中,画出△ABC向下平移4个单位长度得到△A![]() B
B![]() C
C![]() ,点C
,点C![]() 的坐标是________.
的坐标是________.
(2) 在备用图(2)中,以点B为位似中心,在网格内画出△A![]() B
B![]() C
C![]() ,使△A
,使△A![]() B
B![]() C
C![]() 与△ABC位似,且位似比为2︰1,点C
与△ABC位似,且位似比为2︰1,点C![]() 的坐标是________.
的坐标是________.
(3) △A![]() B
B![]() C
C![]() 的面积是________平方单位.
的面积是________平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
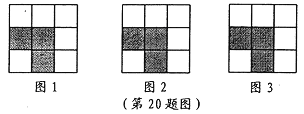
【题目】(本题8分)下列3×3网格都是由9个相同小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形。
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.
(1)图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE=![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a=﹣0.22 , b=﹣2﹣2 , c=(﹣ ![]() )﹣2 , d=(﹣
)﹣2 , d=(﹣ ![]() )0 , 则它们的大小关系是( )
)0 , 则它们的大小关系是( )
A.a<b<c<d
B.b<a<d<c
C.a<d<c<b
D.c<a<d<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4. 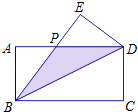
(1)BD=;
(2)点P到BD的距离是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com