
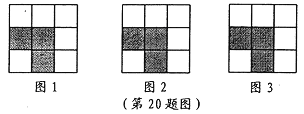
����Ŀ��������8�֣�����3��3��������9����ͬС��������ɣ�ÿ������ͼ����3��С��������Ϳ����Ӱ���������µ�6���հ�С�������У�������Ҫ��Ϳ����Ӱ��
��1��ѡȡ1��Ϳ����Ӱ��ʹ4����ӰС���������һ����Գ�ͼ�Σ����������ĶԳ�ͼ�Σ�
��2��ѡȡ1��Ϳ����Ӱ��ʹ4����ӰС���������һ�����ĶԳ�ͼ�Σ���������Գ�ͼ�Σ�
��3��ѡȡ2��Ϳ����Ӱ��ʹ5����ӰС���������һ����Գ�ͼ�Ρ�
���뽫����С������������ͼ1��ͼ2��ͼ3�У���ֻ�軭������������һ�����Σ�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
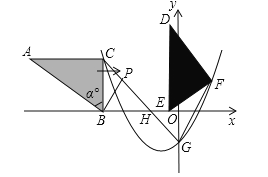
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC����������ֱ���A����8��3����B����4��0����C����4��3������ABC=���㣮������![]() ������C���ҶԳ���Ϊx=
������C���ҶԳ���Ϊx=![]() ������y�ύ�ڵ�G��
������y�ύ�ڵ�G��
��1���������ߵĽ���ʽ����G�����ꣻ
��2����Rt��ABC��x������ƽ��m����λ��ʹB���Ƶ���E��Ȼ���������Ƶ�E˳ʱ����ת����õ���DEF������Fǡ�������������ϣ�
����m��ֵ��
������CG��x���ڵ�H������FG����B��BP��FG����CG�ڵ�P����֤��PH=GH��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڡ�ABC�У���ACB=90�㣬��D��E�ֱ�ΪAC��AB���е㣬��F��BC���ӳ����ϣ��ҡ�CDF=��A����֤���ı���DECFΪƽ���ı��Σ� 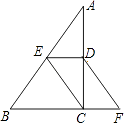
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
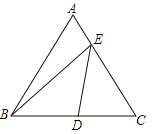
����Ŀ����ͼ���ڱ߳�Ϊ2�ĵȱߡ�ABC�У�DΪBC���е㣬E��AC����һ�㣬��BE+DE����СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȷ���ǣ�������
A. b3b3=2b3 B. x2x3=x6 C. ��a5��2=a7 D. a5��a2=a3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���E��BC�ϣ�CD��AB��EF��AB������ֱ�ΪD��F��
��1��CD��EFƽ����Ϊʲô��
��2�������1=��2���ҡ�3=115�㣬���ACB�Ķ����� 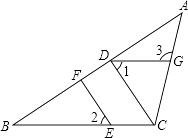
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У��١�A+��B=��C�� �ڡ�A����B����C=1��2��3�� �ۡ�A= ![]() ��B=
��B= ![]() ��C�� �ܡ�A=��B=2��C�� �ݡ�A=2��B=3��C����ȷ����ABCΪֱ�������ε������У� ��
��C�� �ܡ�A=��B=2��C�� �ݡ�A=2��B=3��C����ȷ����ABCΪֱ�������ε������У� ��
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ��⡣
��1����ͼ�٣���ABC�У���D��E�ڱ�BC�ϣ�AEƽ�֡�BAC��AD��BC����C=40�㣬��B=60�㣬�١�CAE�Ķ������ڡ�DAE�Ķ�����
��2����ͼ�ڣ����ѣ�1���е�������AD��BC����ɡ�FΪAE�ӳ�����һ�㣬��FD��BC���������������䣬�����DFE�Ķ�����
��3���ڡ�ABC�У�AEƽ�֡�BAC����FΪEA�ӳ�����һ�㣬FD��BC���ҡ�C=������B=�£��£��������Բ����DFE�Ķ������æ����±�ʾ�������Լ�������Ӧͼ�β�˵�����ɣ� 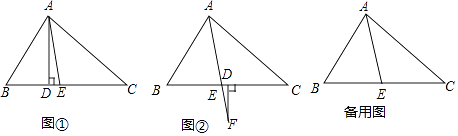
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com