
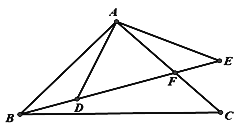
【题目】如图,点B、D、E在一条直线上,BE与AC相交于点F,且![]()
⑴求证:△ABC∽△ADE;
⑵求证:∠BAD=∠CAE;
⑶若∠BAD=18°,求∠EBC的度数.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线C1:![]() 与x轴的一个交点为A(-1,0),另一个交点为B,与
与x轴的一个交点为A(-1,0),另一个交点为B,与![]() 轴的交点为C(0,-3),其顶点为D.
轴的交点为C(0,-3),其顶点为D.
(1)求抛物线C1的解析式;
(2)如图1,将△OBC沿![]() 轴向右平移m个单位长度(0﹤
轴向右平移m个单位长度(0﹤![]() ≤
≤![]() )得到另一个三角形△EFG,将△EFG与△BCD重叠部分(四边形BPGQ)的面积记为S,用含m的代数式表示S;
)得到另一个三角形△EFG,将△EFG与△BCD重叠部分(四边形BPGQ)的面积记为S,用含m的代数式表示S;
(3)如图2,将抛物线C1平移,使其顶点为原点O,得到抛物线C2.若直线![]() 与抛物线C2交于S、T两点,点
与抛物线C2交于S、T两点,点![]() 是线段ST上一动点(不与S、T重合),试探究抛物线C2上是否存在一点R,点R关于点N的中心对称点K也在抛物线C2上.
是线段ST上一动点(不与S、T重合),试探究抛物线C2上是否存在一点R,点R关于点N的中心对称点K也在抛物线C2上.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交,其顶点坐标为
轴正半轴相交,其顶点坐标为![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有两个相等的实数根,其中正确的结论是________.(只填序号即可).
有两个相等的实数根,其中正确的结论是________.(只填序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() ,
,![]() 运动的时间是
运动的时间是![]() (
(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.

(1)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,请说明理由;
值;如果不能,请说明理由;
(2)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() .回答下列问题:
.回答下列问题:
(1)求出它的图像与坐标轴的交点坐标;
(2)当自变量![]() 满足什么条件时?函数值
满足什么条件时?函数值![]() ?
?
(3)当自变量![]() 时,则函数值
时,则函数值![]() 的范围?
的范围?
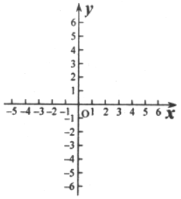
(4)在所给的直角坐标系中,画出直线![]() 的图像.
的图像.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com