
【题目】如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA= ![]() ,cot∠ABC=
,cot∠ABC= ![]() ,AD=8.
,AD=8.
(1)求⊙D的半径;
(2)求CE的长.
【答案】
(1)
【答案】解:∵CD⊥AB,AD=8,tanA= ![]() ,
,
在Rt△ACD中,tanA= ![]() =
= ![]() ,AD=8,CD=4,
,AD=8,CD=4,
在Rt△CBD,cot∠ABC= ![]() =
= ![]() ,BD=3,
,BD=3,
∴⊙D的半径为3
(2)
解:过圆心D作DH⊥BC,垂足为H,
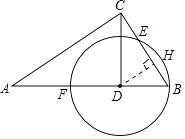
∴BH=EH,
在Rt△CBD中∠CDB=90°,BC= ![]() =5,cos∠ABC=
=5,cos∠ABC= ![]() =
= ![]() ,
,
在Rt△BDH中,∠BHD=90°,cos∠ABC= ![]() =
= ![]() ,BD=3,BH=
,BD=3,BH= ![]() ,
,
∵BH=EH,
∴BE=2BH= ![]() ,
,
∴CE=BC﹣BE=5﹣ ![]() =
= ![]() .
.
【解析】(1)根据三角函数的定义得出CD和BD,从而得出⊙D的半径;
(2)过圆心D作DH⊥BC,根据垂径定理得出BH=EH,由勾股定理得出BC,再由三角函数的定义得出BE,从而得出CE即可.
【考点精析】认真审题,首先需要了解垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的顶点B在反比例函数 ![]() 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( )
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( ) 
A.12
B.4 ![]()
C.12-3 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
数学活动课上,老师出了一道作图问题:“如图,已知直线l和直线l外一点P.用直尺和圆规作直线PQ,使PQ⊥l于点Q.”

小艾的作法如下:
(1)在直线l上任取点A,以A为圆心,AP长为半径画弧.
(2)在直线l上任取点B,以B为圆心,BP长为半径画弧.
(3)两弧分别交于点P和点M
(4)连接PM,与直线l交于点Q,直线PQ即为所求.
老师表扬了小艾的作法是对的.
请回答:小艾这样作图的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使得点A落在点A'处,当A'E⊥AC时,A'B= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“626国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作如表频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:
少分数段(x表示分数) | 频数 | 频率 |
50≤x<60 | 4 | 0.1 |
60≤x<70 | a | 0.2 |
70≤x<80 | 12 | b |
80≤x<90 | 10 | 0.25 |
90≤x<100 | 6 | 0.15 |

(1)表中a= , b= , 并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段80≤x<100对应扇形的圆心角度数是;
(3)请估计该年级分数在60≤x<100的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF. 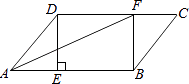
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,拦水坝的横断面为梯形ABCD,AB∥CD,坝顶宽DC为6米,坝高DG为2米,迎水坡BC的坡角为30°,坝底宽AB为(8+2 ![]() )米.
)米. 
(1)求背水坡AD的坡度;
(2)为了加固拦水坝,需将水坝加高2米,并且保持坝顶宽度不变,迎水坡和背水坡的坡度也不变,求加高后坝底HB的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹): 
(1)作△ABC的外心O;
(2)设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com