
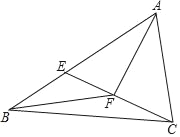
【题目】△ABC中,AB=CB,AC=10,S△ABC=60,E为AB上一动点,连结CE,过A作AF⊥CE于F,连结BF,则BF的最小值是_____.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.

(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() 都为等腰直角三角形,
都为等腰直角三角形,![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() .
.

(1)若![]() ,求
,求![]() 的周长;
的周长;
(2)如图![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长至
并延长至![]() ,使得
,使得![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
②探索![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
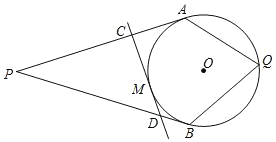
【题目】如图,PA、PB分别切⊙O于点A、B,M为劣弧AB上一点(不与A、B重合)过点M的切线分别与PA、PB相交于点C、D,Q为优弧AB上一点(不与A、B重合).
(1)若PA=10,求△PCD的周长;
(2)若∠P=40°,求∠AQB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
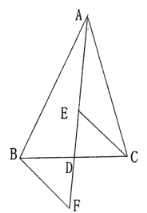
【题目】如图,![]() 是
是![]() 的中线,
的中线,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 延长线上的点,且
延长线上的点,且![]() ,连接
,连接![]() 、
、![]() ,下列说法:①
,下列说法:①![]() 和
和![]() 的面积相等,②
的面积相等,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,其中一定正确的答案有______________.(只填写正确的序号)
,其中一定正确的答案有______________.(只填写正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了![]() ,
,![]() 两种型号的空气净化器,已知一台
两种型号的空气净化器,已知一台![]() 型空气净化器的进价比一台
型空气净化器的进价比一台![]() 型空气净化器的进价多300元,用7500元购进
型空气净化器的进价多300元,用7500元购进![]() 型空气净化器和用6000元购进
型空气净化器和用6000元购进![]() 型空气净化器的台数相同.
型空气净化器的台数相同.
(1)求一台![]() 型空气净化器和一台
型空气净化器和一台![]() 型空气净化器的进价各为多少元?
型空气净化器的进价各为多少元?
(2)在销售过程中,![]() 型空气净化器因为净化能力强,噪声小而更受消费者的欢迎.商社电器计划
型空气净化器因为净化能力强,噪声小而更受消费者的欢迎.商社电器计划![]() 型净化器的进货量不少于20台且是
型净化器的进货量不少于20台且是![]() 型净化器进货量的三倍,在总进货款不超过5万元的前提下,试问有多少种进货方案?
型净化器进货量的三倍,在总进货款不超过5万元的前提下,试问有多少种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
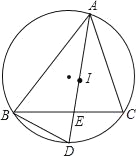
【题目】如图,点I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,与BC相交于点E.
(1)求证:DI=DB;
(2)若AE=6cm,ED=4cm,求线段DI的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
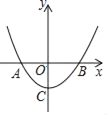
【题目】如图,二次函数y=x2﹣m2(m>0且为常数)的图象与x轴交于点A、B(A在B左侧),与y轴交于C.
(1)求A,B,C三点的坐标(用含m的式子表示);
(2)若∠ACB=90°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com