
【题目】已知,△ABC中,∠C=90°.

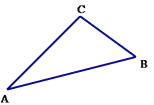
(1)若AC=4,BC=3,AE=![]() ,DE⊥AC.且DE=DB,求AD的长;
,DE⊥AC.且DE=DB,求AD的长;
(2)请你用没有刻度的直尺和圆规,在线段AB上找一点F,使得点F到边AC的距离等于FB(注:不写作法,保留作图痕迹,对图中涉及到的点的用字母进行标注)
科目:初中数学 来源: 题型:
【题目】已知某市2016年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.

(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2016年10月份的水费为620元,求该企业2016年10月份的用水量;
(3)为鼓励企业节约用水,该市自2017年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2016年收费标准收取水费外,超过80吨的部分每吨另加收![]() 元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
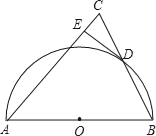
【题目】如图,半圆O的直径为AB,D是半圆上的一个动点(不与点A,B重合),连接BD并延长至点C,使CD=BD,连接AC,过点D作DE⊥AC于点E.
(1)请猜想DE与⊙O的位置关系,并说明理由;
(2)当AB=4,∠BAC=45°时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善交通拥堵状况,我市进行了大规模的道路桥梁建设.已知某路段乙工程队单独完成所需的天数是甲工程队单独完成所需天数的1.5倍,如果按甲工程队单独工作20天,再由乙工程队单独工作30天的方案施工,这样就完成了此路段的![]() .
.
(1)求甲、乙工程队单独完成这项工程各需多少天?
(2)已知甲工程队每天的施工费用是2万元,乙工程队每天的施工费用为1.2万元,要使该项目的工程费不超过114万元,则需要改变施工方案,但甲乙两个工程队不能同时施工,乙工程队最少施工多少天才能完成此项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
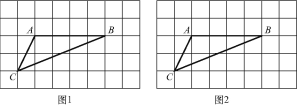
【题目】如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A,B,C,D为顶点的四边形是轴对称图形;
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A,B,C,E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,己知O为坐标原点,点A(3,0),B(0.4),以点A为旋转中心,把△ABO顺时针旋转,得△ACD.记旋转角为α.∠ABO为β.

(I )如图①,当旋转后点D恰好落在AB边上时,求点D的坐标;
(II)如图②,当旋转后满足BC∥x轴时,求α与β之间的数量关系:
(III)当旋转后满足∠AOD=β时,求直线CD的解析式(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
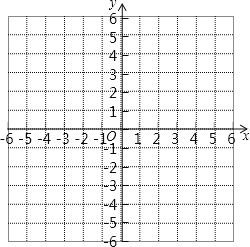
【题目】已知二次函数 y=2x2-8x+6.
(1)利用配方法写出这个函数图象的开口方向、对称轴、顶点坐标.
(2)在下面的平面直角坐标系中画图此函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,正方形ABCD中,AD=4,点E在CD上,DE=3CE,F是AD上异于D的点,且∠EFB=∠FBC,则tan∠DFE=( )

A. 2![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com