
【题目】对于二次函数y=x2﹣2mx﹣3,有下列说法:
①它的图象与x轴有两个公共点;
②如果当x≤1时y随x的增大而减小,则m=1;
③如果将它的图象向左平移3个单位后过原点,则m=﹣1;
④如果当x=4时的函数值与x=2008时的函数值相等,则当x=2012时的函数值为﹣3.
其中正确的说法是_____.(把你认为正确说法的序号都填上)
【答案】①④
【解析】
①根据函数与方程的关系解答;②找到二次函数的对称轴,再判断函数的增减性;③将m=-1代入解析式,求出和x轴的交点坐标,即可判断;④根据坐标的对称性,求出m的值,得到函数解析式,将m=2012代入解析式即可.
①∵△=4m2-4×(-3)=4m2+12>0,∴它的图象与x轴有两个公共点,故①正确;
②∵当x≤1时y随x的增大而减小,函数的对称轴x=-![]() ≥1,
≥1,
∴在直线x=1的右侧(包括与直线x=1重合),
则-![]() ≥1,即m≥1,故②错误;
≥1,即m≥1,故②错误;
③将m=-1代入解析式,得y=x2+2x-3,当y=0时,得x2+2x-3=0,即(x-1)(x+3)=0,
解得,x1=1,x2=-3,将图象向左平移3个单位后不过原点,故③错误;
④∵当x=4时的函数值与x=2008时的函数值相等,
∴对称轴为x=![]() =1006,
=1006,
则-![]() =1006,m=1006,
=1006,m=1006,
原函数可化为y=x2-2012x-3,当x=2012时,y=20122-2012×2012-3=-3,故④正确,
故答案为:①④.


科目:初中数学 来源: 题型:
【题目】为了“迎国庆,向祖国母亲献礼”,某建筑公司承建了修筑一段公路的任务,指派甲、乙两队合作,18天可以完成,共需施工费126000元;如果甲、乙两队单独完成此项工程,乙队所用时间是甲队的1.5倍,乙队每天的施工费比甲队每天的施工费少1000元.
(1)甲、乙两队单独完成此项工程,各需多少天?
(2)为了尽快完成这项工程任务,甲、乙两队通过技术革新提高了速度,同时,甲队每天的施工费提高了![]() ,乙队每天的施工费提高了
,乙队每天的施工费提高了![]() ,已知两队合作12天后,由甲队再单独做2天就完成了这项工程任务,且所需施工费比计划少了21200元.
,已知两队合作12天后,由甲队再单独做2天就完成了这项工程任务,且所需施工费比计划少了21200元.
①分别求出甲、乙两队技术革新前每天的施工费用;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;
∠C;
②AE+BF=EF;
③当∠C=90°时,E,F分别是AC,BC的中点;
④若OD=a,CE+CF=2b,则S△CEF=ab.
其中正确的是( )

A.①②B.③④C.①②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.
(1)若△BCD的周长为8,求BC的长;
(2)若∠A=40°,求∠DBC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从
两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从![]() 地匀速开往
地匀速开往![]() 地,乙车从
地,乙车从![]() 地沿此公路匀速开往
地沿此公路匀速开往![]() 地,两车分别到达目的地后停止甲、乙两车相距的路程
地,两车分别到达目的地后停止甲、乙两车相距的路程![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (时)之间的函数关系如图所示:
(时)之间的函数关系如图所示:

(1)乙年的速度为______千米/时,![]() _____,
_____,![]() ______.
______.
(2)求甲、乙两车相遇后![]() 与
与![]() 之间的函数关系式,并写出相应的自变量
之间的函数关系式,并写出相应的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON![]() 60°,点A是OM边上一点,点B,C是ON边上两点,且AB
60°,点A是OM边上一点,点B,C是ON边上两点,且AB![]() AC,作点B关于OM的对称点点D,连接AD,CD,OD.
AC,作点B关于OM的对称点点D,连接AD,CD,OD.
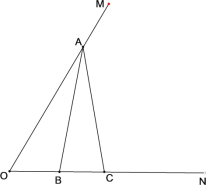

(1)依题意补全图形;
(2)猜想∠DAC![]() °,并证明;
°,并证明;
(3)猜想线段OA、OD、OC的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,连接
边上,连接![]() ,连接
,连接![]()

(1)求证:![]()
(2)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]()
①补全图形并证明![]()
②利用备用图进行画图、试验、探究,找出当![]() 三点恰好共线时点
三点恰好共线时点![]() 的位置,请直接写出此时
的位置,请直接写出此时![]() 的度数,并画出相应的图形
的度数,并画出相应的图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生共900人,为了解这个年级学生的体能,从中随机抽取部分学生进行1 min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理,下图是这四名同学提供的部分信息:
甲:将全体测试数据分成6组绘成直方图(如图);
乙:跳绳次数不少于105次的同学占96%;
丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是12;
丁:第②、③、④组的频数之比为4:17:15。

根据这四名同学提供的材料,下面有四个推断:
①这次跳绳测试共抽取了150人;②该年级跳绳次数的中位数在115~125之间
③第4组的人数为45人 ④如果跳绳次数不少于135次为优秀,根据这次调查结果,估计全年级达到跳绳优秀的人数可以超过250人,其中合理的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.
ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.

(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com