
分析 由于符合要求的三角形不唯一,需分情况讨论.可按30°角的对边的长度进行分类:①若30°角的对边的长度既不是5又不是4,②若30°角的对边的长度是4,③若30°角的对边的长度是5.结合画图就可解决问题.
解答 解:符合条件的三角形共有四个.
理由如下:
①若30°角的对边的长度既不是5又不是4,
作∠MAN=30°,在AM上取一点B使得AB=5,在AN上取一点C使得AC=4,连接BC,如图1.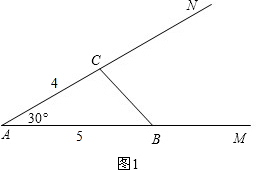
由SAS可得这样的三角形只有一个.
②若30°角的对边的长度是4,
如图2和图3.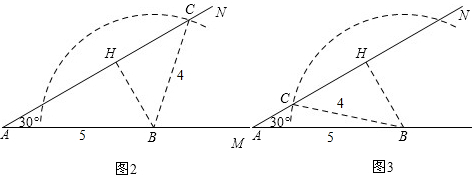
可见这样的三角形有两个.
③若30°角的对边的长度是5,
如图4.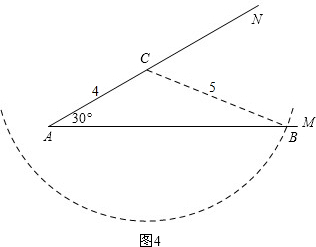
可见这样的三角形只有一个.
综上所述:符合条件的三角形共有四个.
故答案为:4.
点评 本题考查了三角形的边角关系、30°角所对的直角边等于斜边的一半、直线与圆的位置关系、全等三角形的判定(SAS)等知识,考查了动手操作的能力,还考查了分类讨论的思想,而选择一个适当的分类标准是解决本题的关键.


科目:初中数学 来源: 题型:解答题
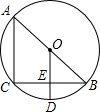 如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交$\widehat{CB}$于D,连接AC、BD.
如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交$\widehat{CB}$于D,连接AC、BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
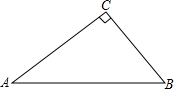 如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6.若P、Q分别是AB和AC上的动点,则PC+PQ的最小值是$\frac{192}{25}$.
如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6.若P、Q分别是AB和AC上的动点,则PC+PQ的最小值是$\frac{192}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
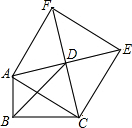 如图,在△ABC中,∠ABC=90°,以AC为一边向三角形外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,BD平分∠ABC.
如图,在△ABC中,∠ABC=90°,以AC为一边向三角形外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,BD平分∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
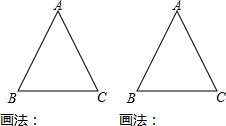 晓明有一把没有刻度的直角三角板,他要用这块三角板找出一个等腰三角形的对称轴,你能帮他完成吗?请用两种方法在图中画出等腰三角形的对称轴并注明方法.
晓明有一把没有刻度的直角三角板,他要用这块三角板找出一个等腰三角形的对称轴,你能帮他完成吗?请用两种方法在图中画出等腰三角形的对称轴并注明方法.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com