
【题目】对于三个数![]() 、
、![]() 、
、![]() ,用
,用![]() 表示这三个数的中位数,用
表示这三个数的中位数,用![]() 表示这三个数中最大数,例如:
表示这三个数中最大数,例如:![]() ,
,![]() ,
,![]() .
.
解决问题:
(1)填空:![]() ,如果
,如果![]() ,则
,则![]() 的取值范围为 ;
的取值范围为 ;
(2)如果![]() ,求
,求![]() 的值;
的值;
(3)如果![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)﹣3或0;(3) x=3或﹣3.
;(2)﹣3或0;(3) x=3或﹣3.
【解析】析:(1)根据定义写出sin45°,cos60°,tan60°的值,确定其中位数;根据max{a,b,c}表示这三个数中最大数,对于max{3,53x,2x6}=3,可得不等式组:则![]() ,可得结论;
,可得结论;
(2)根据新定义和已知分情况讨论:①2最大时,x+4≤2时,②2是中间的数时,x+2≤2≤x+4,③2最小时,x+2≥2,分别解出即可;
(3)不妨设y1=9,y2=x2,y3=3x2,画出图象,根据M{9,x2,3x2}=max{9,x2,3x2},可知:三个函数的中间的值与最大值相等,即有两个函数相交时对应的x的值符合条件,结合图象可得结论.
(1)∵sin45°=![]() ,cos60°=
,cos60°=![]() ,tan60°=
,tan60°=![]() ,
,
∴M{sin45°,cos60°,tan60°}=![]() ,
,
∵max{3,5﹣3x,2x﹣6}=3,
则![]() ,
,
∴x的取值范围为:![]() ,
,
故答案为:![]() ,
,![]() ;
;
(2)2M{2,x+2,x+4}=max{2,x+2,x+4},
分三种情况:①当x+4≤2时,即x≤﹣2,
原等式变为:2(x+4)=2,x=﹣3,
②x+2≤2≤x+4时,即﹣2≤x≤0,
原等式变为:2×2=x+4,x=0,
③当x+2≥2时,即x≥0,
原等式变为:2(x+2)=x+4,x=0,
综上所述,x的值为﹣3或0;
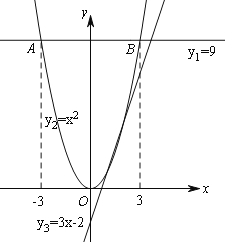
(3)不妨设y1=9,y2=x2,y3=3x﹣2,画出图象,如图所示:
结合图象,不难得出,在图象中的交点A、B点时,满足条件且M{9,x2,3x﹣2}=max{9,x2,3x﹣2}=yA=yB,
此时x2=9,解得x=3或﹣3.


科目:初中数学 来源: 题型:
【题目】如图,A、B两点在数轴上,点A表示的数为–10,OB=4OA,点M以每秒2个单位长度的速度从点A开始向左运动,点N以每秒3个单位长度的速度从点B开始向左运动(点M和点N同时出发).

(1)数轴上点B对应的数是__________,线段AB的中点C对应的数是__________;
(2)经过几秒,点M、点N到原点的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的顶点
的顶点![]() 在第一象限,点
在第一象限,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() 与
与![]() 关于点
关于点![]() 成中心对称,则点
成中心对称,则点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠B+∠BCD=180°,∠B=∠D.

求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD ( )
∴∠B=_______( )
又∵∠B=∠D(已知 ),
∴∠D=_______( )
∴AD∥BE( )
∴∠E=∠DFE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
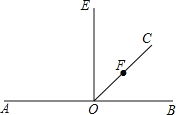
【题目】如图,O为直线AB上一点,F为射线OC上一点,OE⊥AB.
(1)用量角器和直角三角尺画∠AOC的平分线OD,画FG⊥OC,FG交AB于点G;
(2)在(1)的条件下,比较OF与OG的大小,并说明理由;
(3)在(1)的条件下,若∠BOC=40°,求∠AOD与∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
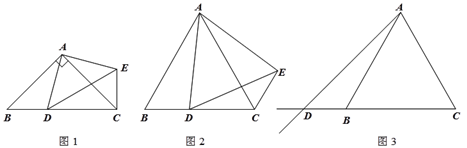
【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC= ![]() ,∠DCE=
,∠DCE= ![]() .
.
① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时![]() 与
与![]() 之间的数量关系(不需证明).
之间的数量关系(不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
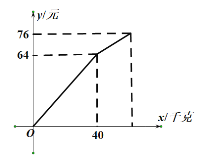
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com