
【题目】如图.抛物线![]() 经过
经过![]() 三点.
三点.
(1)求抛物线的函数关系式;
(2)若直线![]() 是抛物线的对称轴,设点
是抛物线的对称轴,设点![]() 是直线
是直线![]() 上的一个动点,当
上的一个动点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标;
的坐标;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得以线段
,使得以线段![]() 为直径的圆与边
为直径的圆与边![]() 交于
交于![]() 点(与点
点(与点![]() 不同),且以
不同),且以![]() 点为顶点的三角形是等腰三角形?若存在,求出
点为顶点的三角形是等腰三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可.
(2)由图知:A、B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知:若连接BC,那么BC与直线l的交点即为符合条件的P点.
(3)由于△QBO的腰和底没有明确,因此要分三种情况来讨论:①QB=BO、②QB=QO、③QO=BO;可先设出M点的坐标,然后用M点纵坐标表示△QBO的三边长,再按上面的三种情况列式求解即可.
![]() 解:
解:![]() 经过
经过![]()
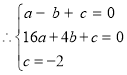
解之得: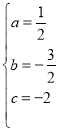
![]() 函数解析式为
函数解析式为![]()
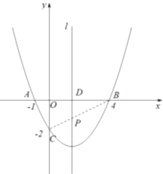
![]() 如图,抛物线的对称轴是直线
如图,抛物线的对称轴是直线![]()
当点![]() 落在线段
落在线段![]() 上时,
上时,
![]() 最小,
最小,![]() 的周长最小.
的周长最小.
设抛物线的对称轴与![]() 轴的交点为
轴的交点为![]()
![]()
![]()
又![]() ,得
,得![]()
由![]()
得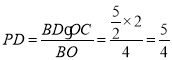
所以点![]() 的坐标为
的坐标为![]()
![]() 过点
过点![]() 作
作![]() 交
交![]() 于点
于点![]()
则根据直径所对圆周角是直角的性质,知点![]() 在以
在以![]() 为直径的圆上
为直径的圆上
由![]()
可证![]() 是直角三角形
是直角三角形
得![]()
![]()
![]()
![]()
由![]() 可得
可得
![]()
则![]()
由![]() ,得
,得![]()
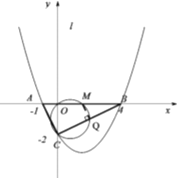
分三种情况:
①当![]() 时,
时,
点![]() 在
在![]() 垂直平分线上,是
垂直平分线上,是![]() 的中点,
的中点,
得![]() .
.
![]()
解得![]()
②当![]() 时,
时, ![]()
![]()
解得:![]()
③当![]() 时,
时,
由于![]() ,
,![]()
从而点![]() 在
在![]() 的延长线上,
的延长线上,
这样点![]() 不在线段
不在线段![]() 上
上
综上所述,![]() 的值为
的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
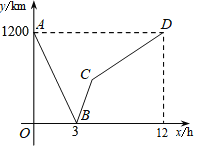
【题目】一列高铁列车从甲地匀速驶往乙地,一列特快列车从乙地匀速驶往甲地,两车同时出发,设特快列车行驶的时间为x(单位:时),特快列车与高铁列车之间的距离为y(单位:千米),y与x之间的函数关系如图所示,则图中线段CD所表示的y与x之间的函数关系式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会为了解本校学生每天做作业所用的时间情况,采用问卷的方式对一部分学生进行调查,在确定调查对象时,大家提出以下几种方案:
(A)对各班班长进行调查;
(B)对某班的全体学生进行调查;
(C)从全校每班随机抽取5名学生进行调查.
在问卷调查时,每位被调查的学生都选择了问卷中适合自己的一个时间,学生会收集到的数据整理后绘制成如图所示的条形统计图.

(1)为了使收集到的数据具有代表性,学生会在确定调查对象时选择了方案____(填A或B或C);
(2)被调查的学生每天做作业所用的时间的众数为_______小时,中位数为______小时;
(3)根据以上统计结果,估计该校800名学生中每天做作业时间用1.5小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=![]() AB.
AB.

探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=![]() AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣![]() ,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
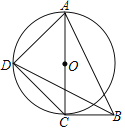
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径作⊙O,D为⊙O上一点,连接AD、BD、CD,且BD=AB
(1)求证:∠ABD=2∠BDC;
(2)若D为弧AC的中点,求tan∠BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
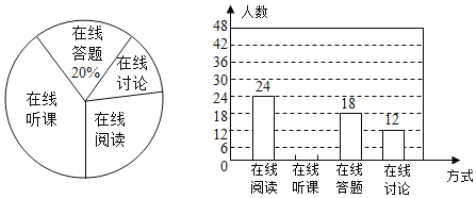
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生2700人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
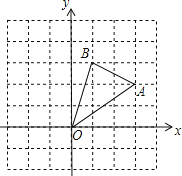
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到A1OB1.
(1)画出旋转后的图形;
(2)点A1的坐标为 ;
(3)求线段OB在旋转过程中所扫过的图形面积(写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com