
| 3 |
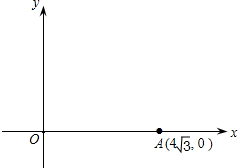 第一象限,且cos∠OPA=
第一象限,且cos∠OPA=| 1 |
| 2 |
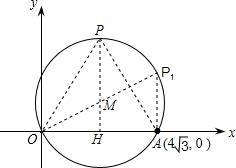 解:(1)如图,作Rt△OP1A,使∠P1AO=90°,∠P1OA=30°,则∠OP1A=60°,
解:(1)如图,作Rt△OP1A,使∠P1AO=90°,∠P1OA=30°,则∠OP1A=60°,| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
|
|
| 1 |
| 2 |
| 3 |
| x | 4
|
2
|
3
|
|
… | ||||||||
| y | 4 | 6 | 2+
|
2+
|
… |


科目:初中数学 来源: 题型:
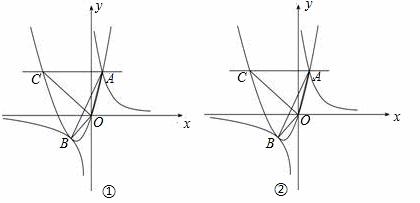
如图,抛物线y=ax2+bx(a>0)与反比例函数![]() 的图象相交于点A,B.已知点A的坐
的图象相交于点A,B.已知点A的坐
为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点).
(1)求反比例函数的解析式;
(2)用含t的代数式表示直线AB的解析式;
(3)求抛物线的解析式;
(4)过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,把△AOB绕点O顺时针旋转90°,请在图②中画出旋转后的三角形,并直接写出所有满足△EOC∽△AOB的点E的坐标.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(山东东营卷)数学(解析版) 题型:解答题
已知抛物线 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线  上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.

查看答案和解析>>
科目:初中数学 来源:2013届安徽滁州八年级下期末模拟数学试卷(沪科版)(解析版) 题型:解答题
已知:如图1,平面直角坐标系 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐
标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
(1)在点D运动的过程中,若△ODE的面积为S,求S与 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.求证:四边形DMEN是菱形;
(3)问题(2)中的四边形DMEN中,ME的长为____________.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com