
【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°. 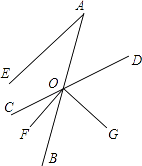
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
【答案】
(1)解:∵AE∥OF,
∴∠FOB=∠A=30°,
∵OF平分∠BOC,
∴∠COF=∠FOB=30°,
∴∠DOF=180°﹣∠COF=150°
(2)解:∵OF⊥OG,
∴∠FOG=90°,
∴∠DOG=∠DOF﹣∠FOG=150°﹣90°=60°,
∵∠AOD=∠COB=∠COF+∠FOB=60°,
∴∠AOD=∠DOG,
∴OD平分∠AOG
【解析】(1)根据两直线平行,同位角相等可得∠FOB=∠A=30°,再根据角平分线的定义求出∠COF=∠FOB=30°,然后根据平角等于180°列式进行计算即可得解;(2)先求出∠DOG=60°,再根据对顶角相等求出∠AOD=60°,然后根据角平分线的定义即可得解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转后,得到△ADF,此时点D落在边BC的中点处,则图中与∠C相等的角(除∠C外)有( )

A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1,且其对称轴分别交抛物线C,C1于点B1,D1,此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2,且其对称轴分别交抛物线C1,C2于点B2,D2,此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3.请探究以下问题:
(1)填空:a1= ,b1= ;
(2)求出C2与C3的解析式;
(3)按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题:
(1)计算下列各式:
① ![]() = ,
= , ![]() =;
=;
② ![]() = ,
= , ![]() = .
= .
通过计算,我们可以发现 ![]() =
=
(2)运用(1)中的结果可以得到: ![]()
![]() =×=
=×=
(3)通过(1)(2),完成下列问题:
①化简: ![]() ;
;
②计算: ![]() ;
;
③化简 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度数;(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示.
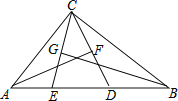
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com