
【题目】如图,在△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转后,得到△ADF,此时点D落在边BC的中点处,则图中与∠C相等的角(除∠C外)有( )

A.5个 B.4个 C.3个 D.2个
【答案】A
【解析】
试题分析:根据旋转得出∠C=∠FDA,AC=AD,根据直角三角形性质得出AD=DC,求出△ADC是等边三角形,即可求出∠ADC=∠DAC=∠FDB=∠FDA=∠FAB=60°,即可得出选项.∵将△ABC绕点A顺时针旋转后,得到△ADF,∴∠C=∠FDA,AC=AD, ∵∠BAC=90°,D为BC的中点, ∴AD=DC, ∴∠C=∠DAC,AD=AC=CD,
∴△ADC是等边三角形, ∴∠DAC=∠C=∠ADC=60°, ∴∠FDA=∠C=60°,
∴∠B=30°,∠FDB=180°﹣60°﹣60°=60°, ∴∠F=∠B=30°,∠AEF=∠BED=90°,
∴∠FAB=180°﹣90°﹣30°=60°, 即∠C=∠ADC=∠DAC=∠FDB=∠FDA=∠FAB=60°,
即和∠C相等的角有5个,


科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.利用数形结合思想回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 , 数轴上表示2和﹣3的两点之间的距离是
(2)数轴上表示x和﹣2的两点之间的距离表示为 .
(3)若x表示一个有理数,且﹣4≤x≤﹣2,则|x﹣2|+|x+4|=
(4)若|x+3|+|x﹣5|=8,利用数轴求出x的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)作图:在△BED中作出BD边上的高EF;BE边上的高DG;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高EF为多少?若BE=6,求△BED中BE边上的高DG为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第六届世界数学团体锦标赛于2015年11月25日至11月29日在北京举行,其会徽如图所示,它的内围与外围分别是由七个与四边形ABCD全等的四边形和七个与四边形BEFC全等的四边形依次环绕而成的正七边形.设AD=a,AB=b,CF=c,EF=d,则该会徽内外两个正七边形的周长之和为( )

A.7(a+b+c﹣d) B.7(a+b﹣c+d)
C.7(a﹣b+c+d) D.7(b+c+d﹣a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校就“遇见老人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查(每个被调查的学生必须选择而且只能在4种方式中选择一项),图1和图2是整理数据后绘制的两幅不完整的统计图,请根据图中提供的信息,解答下列问题: 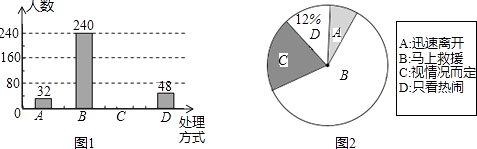
(1)该校随机抽查了名学生;
(2)将图1补充完整,在图2中,“视情况而定”部分所占的圆心角是度;
(3)估计该校2800名学生中采取“马上救助”的方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°. 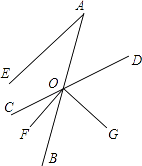
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com