

���� ��1��ֱ��������֪ͼ�α߳�֮��Ĺ�ϵ�ó�y��x֮��Ĺ�ϵ��
��2��ֱ��������֪ͼ�α߳�֮��Ĺ�ϵ�ó�y��x֮��Ĺ�ϵ��
��3��ֱ��������֪��������ʽ�����ó����㣬���ɵó��𰸣�
��� �⣺��1�������⣺5x=3y����y=$\frac{5}{3}x$��
��2�������⣺�߳�Ϊ1cm��С�����εı߳�Ϊ��2x-y��
��2x-y=1��
��3����ͼ��3����ʾ����������Ϊ��3��5����
ʵ��������Ψһ����Լ��ɣ�
��ͼ���£�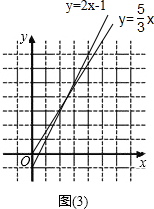 ��
��
���� ������Ҫ������һ�κ�����Ӧ�ã���ȷ�ó�y��x֮��Ĺ�ϵʽ�ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0��m��$\frac{5}{2}$ | B�� | m=-$\frac{1}{2}$ | C�� | -$\frac{1}{2}$��m��0 | D�� | -$\frac{1}{2}$��m��$\frac{5}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -2 | C�� | 2��-1 | D�� | -2��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����A��p��q����0��p��q���ڷ���������y=$\frac{3}{x}$��ͼ���ϣ���OA=5����A��AC��y�ᴹ��ΪC���߶�OA�Ĵ�ֱƽ���߽�OC�ڵ�B������AB�����ABC���ܳ�Ϊ��������
��ͼ����A��p��q����0��p��q���ڷ���������y=$\frac{3}{x}$��ͼ���ϣ���OA=5����A��AC��y�ᴹ��ΪC���߶�OA�Ĵ�ֱƽ���߽�OC�ڵ�B������AB�����ABC���ܳ�Ϊ��������| A�� | 8 | B�� | 7 | C�� | 2$\sqrt{7}$ | D�� | $\sqrt{31}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ����²��ϣ�����������a��b��c����M{a��b��c}��ʾ����������ƽ��������min{a��b��c}��ʾ������������С���������磺
�Ķ����²��ϣ�����������a��b��c����M{a��b��c}��ʾ����������ƽ��������min{a��b��c}��ʾ������������С���������磺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��2 | C�� | x��2 | D�� | x��0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com