
【题目】某校举行“做文明郴州人”演讲比赛,聘请了10位评委为参赛选手打分,赛前,组委会拟定了四种记分方案:方案一:取所有评委所给的平均分;
方案二:在所有评委给的分中,去掉一个最高分,去掉一个最低分,取剩余得分的平均分;
方案三:取所有评委给分的中位数;
方案四:取所有评委给分的众数.
为了探究四种记分方案的合理性,先让一名表演选手(不参加正式比赛的)演讲,让10位评委给演讲者评分,表演者得分如下表:
评委编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
打分 | 7.0 | 7.8 | 3.2 | 8.0 | 8.4 | 8.4 | 9.8 | 8.0 | 8.4 | 8.0 |
(1)请分别用上述四种方案计算表演者的得分;
(2)如果你是评委会成员,你会建议采用哪种可行的记分方案?你觉得哪几种方案不合适?
【答案】(1)方案一最后得分: 7.7;方案二最后得分8;方案三最后得分:8;方案四最后得分:8和8.4.(2)方案1不适合作为最后得分的方案.
【解析】试题分析:(1)根据给出的方案和平均数的计算公式分别进行解答即可;
(2)考虑不受极值的影响,不能有两个得分等原因进行排除,即可得出答案.
试题解析:解:(1)方案一最后得分: ![]() (7.0+7.8+3.2+3×8+3×8.4+9.8)=7.7;
(7.0+7.8+3.2+3×8+3×8.4+9.8)=7.7;
方案二最后得分: ![]() (7.0+7.8+3×8+3×8.4)=8;
(7.0+7.8+3×8+3×8.4)=8;
方案三最后得分:8;
方案四最后得分:8和8.4.
(2)建议采用方案二记分方案.
因为方案1中的平均数受极端数值的影响,不适合作为这个同学演讲的最后得分,所以方案1不适合作为最后得分的方案;
因为方案4中的众数有两个,众数失去了实际意义,所以方案4不适合作为最后得分的方案.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断( )
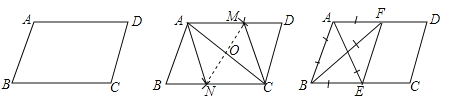
A. 甲正确,乙错误 B. 乙正确,甲错误
C. 甲、乙均正确 D. 甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
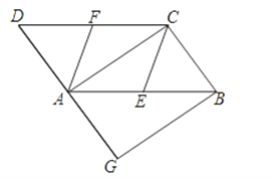
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
(1)求证:CE∥AF;
(2)若∠G=90°,求证:四边形CEAF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球运动员带了2件上衣和3条短裤(上衣和短裤分别装在两个包里),上衣的颜色是红色和白色,短裤的颜色是红色、白色、黄色.
(1)他随意拿出一件上衣和一条短裤配成一套,用画树状图或列表的方法列出所有可能出现的结果.
(2)他随意拿出一件上衣和一条短裤,颜色正好相同的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com