
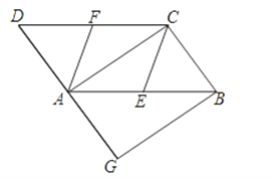
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
(1)求证:CE∥AF;
(2)若∠G=90°,求证:四边形CEAF是菱形.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)根据已知条件证明AE=CF,AE∥CF,从而得出四边形DFBE是平行四边形,即可证明CE∥AF;
(2)先证明CE=AE,再根据邻边相等的平行四边形是菱形,从而得出结论.
试题解析:(1)在□ABCD中,AB∥CD,AB=CD,
∵E、F分别为边AB、CD的中点,
∴CF=![]() CD,AE=
CD,AE=![]() AB,
AB,
∴CF∥AE,CF=AE,
∴四边形CEAF为平行四边形,
∴CE∥AF;
(2)∵BG∥AC,
∴∠G=∠DAC=90°,
∴△DAC为直角三角形,
又∵F为边CD的中点,
∴AF=![]() CD=CF,
CD=CF,
又∵四边形CEAF为平行四边形,
∴四边形CEAF为菱形.


科目:初中数学 来源: 题型:
【题目】在![]() 中,斜边AC的中点M关于BC的对称点O,将△ABC绕点O顺时针旋转至△DCE,连接BD,BE,如图所示.
中,斜边AC的中点M关于BC的对称点O,将△ABC绕点O顺时针旋转至△DCE,连接BD,BE,如图所示.
(1)在①![]() ,②
,②![]() ,③
,③![]() 中,等于旋转角的是 (填出满足条件的角的序号);
中,等于旋转角的是 (填出满足条件的角的序号);
(2)若![]() 求
求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(3)点N是BD的中点,连接MN,用等式表示线段MN与BE之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
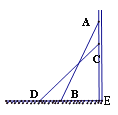
【题目】如图,将长为2.5米长的梯子AB斜靠在墙上,BE长0.7米。
(1)求梯子上端到墙的底端E的距离(即AE的长);
(2)如果梯子的顶端A沿墙下滑0.4米(即AC=0.4米),则梯脚B将外移(即BD长)多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
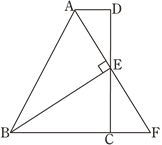
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. 已知AD=2cm,BC=5cm.
(1)求证:FC=AD;
(2)求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 ![]() 的图像如图所示,点A0位于坐标原点,点A1 , A2 , A3 , …,A2008在y轴的正半轴上,点B1 , B2 , B3 , …,B2008在二次函数
的图像如图所示,点A0位于坐标原点,点A1 , A2 , A3 , …,A2008在y轴的正半轴上,点B1 , B2 , B3 , …,B2008在二次函数 ![]() 位于第一象限的图像上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长=
位于第一象限的图像上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“做文明郴州人”演讲比赛,聘请了10位评委为参赛选手打分,赛前,组委会拟定了四种记分方案:方案一:取所有评委所给的平均分;
方案二:在所有评委给的分中,去掉一个最高分,去掉一个最低分,取剩余得分的平均分;
方案三:取所有评委给分的中位数;
方案四:取所有评委给分的众数.
为了探究四种记分方案的合理性,先让一名表演选手(不参加正式比赛的)演讲,让10位评委给演讲者评分,表演者得分如下表:
评委编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
打分 | 7.0 | 7.8 | 3.2 | 8.0 | 8.4 | 8.4 | 9.8 | 8.0 | 8.4 | 8.0 |
(1)请分别用上述四种方案计算表演者的得分;
(2)如果你是评委会成员,你会建议采用哪种可行的记分方案?你觉得哪几种方案不合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)已知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上且OC=2,过点C作直线![]() ∥PQ,点D在点C的左边且CD=3.
∥PQ,点D在点C的左边且CD=3.
(1)直接写出△BCD的面积.
(2)如图②,若AC⊥BC,作∠CBA的平分线交OC于E,交AC于F,则∠CEF与∠CFE有何数量关系?请说明理由.
(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H,在点B运动过程中![]() 的值是否变化?若不变,直接写出其值;若变化,直接写出变化范围.
的值是否变化?若不变,直接写出其值;若变化,直接写出变化范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com