
【题目】如图,在直角坐标系中,点A(0,1),点B(3,0),点C(4,3).
(1)判断△ABC的形状并说明理由;
(2)在线段OC的右侧,以OC为边作等腰直角△OCD,点D的坐标为 .
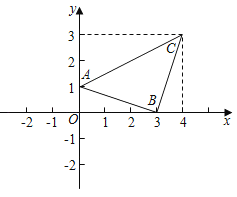
【答案】(1)△ABC是等腰直角三角形,理由详见解析;(2)(3,﹣4),(7,﹣1),(![]() ,﹣
,﹣![]() ) .
) .
【解析】
(1)结论:△ABC是等腰直角三角形.添加辅助线,构造全等三角形解决问题;
(2)分三种情形画出图形即可解决问题.
解:(1)结论:△ABC是等腰直角三角形.
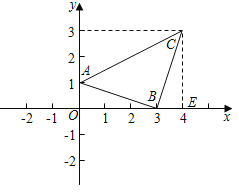
理由:作CE⊥x轴于E.
∵点A(0,1),点B(3,0),点C(4,3),
∴OA=BE=1,OB=CE=3,
∵∠AOB=∠CEB=90°,
∴△AOB≌△BEC(SAS),
∴BA=BC,∠ABO=∠BCE,
∵∠BCE+∠CBE=90°,
∴∠ABO+∠CBE=90°,
∴∠ABC=90°,
∴△ABC是等腰直角三角形.
(2)如图,
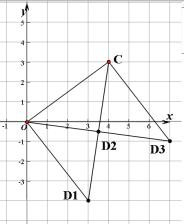
由图象可知:
①当OC为腰,点O为直角顶点时,即OC绕点O顺时针旋转90°,由(1)中正三角形全等的方法,可得D1坐标为(3,﹣4);
②当OC为腰,点C为直角顶点时,即OC绕点C逆时针旋转90°,方法同①,得D3坐标为(7,﹣1;
③当OC是等腰直角三角形的斜边时,因为∠OCD1=∠COD3=45°,所以CD1与OD3的交点即为D2,也是CD1与OD3的中点,可得坐标为(![]() ,﹣
,﹣![]() ).
).
综上:满足条件的点D的坐标分别为(3,﹣4),(7,﹣1),(![]() ,﹣
,﹣![]() ).
).
故答案为(3,﹣4),(7,﹣1),(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.

(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=2,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,弦AB、CD互相垂直,垂足为E,点M在CD上,连接AM并延长交BC于点F,交圆上于点G,连接AD,AD=AM.
(1)如图1,求证:AG⊥BC;
(2)如图2,连接EF,DG,求证:EF∥DG;
(3)如图3,在(2)的条件下,连接BG,若∠ABG=2∠BAG,EF=15,AB=32,求BG长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分) “先学后教”课题组对学生参与小组合作的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.课题组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了______名学生;
(2)请将条形统计图补充完整;
(3)求出扇形统计图中,“主动质疑”所对应扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
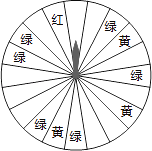
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一种游戏:三张大小,质地都相同的卡片上分别标有数字1,2,3,现将标有数字的一面朝下,小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和,如果和为奇数,则小明胜,若和为偶数则小亮胜.
(1)用列表或画树状图等方法,列出小明和小亮抽得的数字之和所有可能出现的情况.
(2)请判断该游戏对双方是否公平?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为 元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com