
【题目】如图,在⊙O中,弦AB、CD互相垂直,垂足为E,点M在CD上,连接AM并延长交BC于点F,交圆上于点G,连接AD,AD=AM.
(1)如图1,求证:AG⊥BC;
(2)如图2,连接EF,DG,求证:EF∥DG;
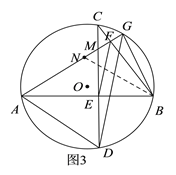
(3)如图3,在(2)的条件下,连接BG,若∠ABG=2∠BAG,EF=15,AB=32,求BG长.

【答案】(1)AG⊥BC;(2)E、F分别为MD、MG中点,EF∥DG ;(3)BG=18
【解析】
试题
(1)由AB⊥CD于点E可得∠B+∠C=90°;由AD=AM,可得∠CMF=∠AMD=∠D=∠B,由此可得∠CMF+∠C=90°,从而得到∠CFM=90°即可得到AG⊥BC;
(2)如图2,连接CG,由AD=AM,AB⊥CD可得点E是DM的中点;由(1)可知∠CMF=∠B,结合∠B=∠CGA,可得∠CMF=∠CGA,从而可得CM=CG,结合(1)中结论AG⊥BC可得点F是MG的中点,由此可得EF是△MDG的中位线,从而可得结论EF∥DG;
(3)如图3,作∠ABG的平分线交AG于点N,由∠ABG=2∠BAG,结合已知条件可证得∠ABG=∠DAG,从而得到AG=DG=2EF=30;由BN平分∠ABG及∠ABG=2∠BAG可得∠GBN=∠ABN=∠GAB,结合∠AGB=∠BGA可证得△GBN∽GAB,BN=AN,设AN=x、BG=y,根据相似三角形的性质列出比例式即可解得BG的值.
试题解析:
(1)∵AB⊥CD于点E,
∴∠BEC=90°,
∴∠B+∠C=90°.
∵AD=AM,
∴∠AMD=∠D=∠B,
又∵∠CMF=∠AMD,
∴∠CMF=∠B,
∴∠CMF+∠C=90°,
∴∠CFM=90°,
∴AG⊥BC;
(2)如图2,连接CG,
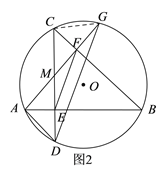
(2)由(1)可知,∠CMF=∠B,
∵∠B=∠CGA,
∴∠CMF=∠G,
∴CM=CG,
又∵AG⊥BC,
∴点F是MG的中点.
∵AD=AM,AB⊥CD,
∴点E是DM的中点,
∴EF是△MDG的中位线,
∴EF∥DG;
(3)∵由(2)可知,EF是△MDG的中位线,EF=15,
∴DG=2EF=30,
∵AD=AM,AB⊥CD,
∴∠DAG=2∠BAG,
又∵∠ABG=2∠BAG,
∴∠ABG=∠DAG,
∴AG=DG=30.
如图3,作BN平分∠ABG,则∠GBN=∠ABN=∠GAB,
∴AN=BN,
∵∠AGB=∠BGA,
∴△GBN∽GAB,
∴![]() ,
,![]() ,
,
设BG=x,AN=BN=y,则GN=AG-AN=30-y,
∴![]() ,
,![]() ,两式变形可得:
,两式变形可得:![]() ,
,
解得:![]() (不合题意,舍去),
(不合题意,舍去),
∴BG=18.


科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是![]() 上一点(不与C、D重合),求证:∠CPD=∠COB;
上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠DCE=β.
(1)如图①,点D在线段BC上移动时,角α与β之间的数量关系是____________,请说明理由;
(2)如图②,点D在线段BC的延长线上移动时,角α与β之间的数量关系是____________,请说明理由;
(3)当点D在线段BC的反向延长线上移动时,请在图③中画出完整图形并猜想角α与β之间的数量关系是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求此抛物线的解析式;
(2)设抛物线的顶点为![]() ,将直线
,将直线![]() 沿
沿![]() 轴向下平移两个单位得到直线
轴向下平移两个单位得到直线![]() ,直线
,直线![]() 与抛物线的对称轴交于
与抛物线的对称轴交于![]() 点,
点,![]() 求直线
求直线![]() 的解析式;
的解析式;
(3)在(2)的条件下,求到直线![]() 距离相等的点的坐标.
距离相等的点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AD∥BC,∠A=90°,∠C=60°,AD=3cm,BC=9cm.⊙O1的圆心O1从点A开始沿折线A﹣D﹣C以1cm/s的速度向点C运动,⊙O2的圆心O2从点B开始沿BA边以![]() cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为t.
(1)请求出⊙O2与腰CD相切时t的值;
(2)在0s<t≤3s范围内,当t为何值时,⊙O1与⊙O2外切?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查,问卷给出了四种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的扇形统计图和条形统计图(均不完整).

根据以上信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生;
(2)补全条形统计图;
(3)如果全校有1200名学生,学习准备的400个自行车停车位是否够用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A(0,1),点B(3,0),点C(4,3).
(1)判断△ABC的形状并说明理由;
(2)在线段OC的右侧,以OC为边作等腰直角△OCD,点D的坐标为 .
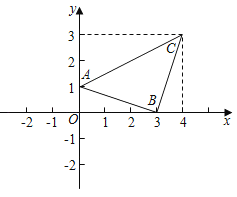
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地_____千米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com