
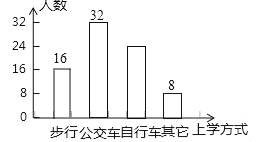
【题目】某校为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查,问卷给出了四种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的扇形统计图和条形统计图(均不完整).

根据以上信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生;
(2)补全条形统计图;
(3)如果全校有1200名学生,学习准备的400个自行车停车位是否够用?
【答案】(1)80;(2)答案见解析;(3)够用。
【解析】
试题(1)根据公交车所占比例为40%,而由条形图知一共有32人坐公交车上学,从而求出总人数;
(2)由扇形统计图知:步行占20%,而由(1)总人数已知,从而求出步行人数,补全条形图;
(3)根据被调查的总人数及骑自行车上学的人数,用样本中骑自行车人数所占比例乘以总人数1200,与的400个自行车停车位比较即可得答案.
试题解析:解:(1)32÷40%=80,故答案为:80;
(2)“步行”的人数为:80×20%=16(人),补全图,如下:
(3)∵骑自行车上学的人有80﹣(16+32+8)=24(人),∴![]() ×1200=360,∵360<400,∴够用.
×1200=360,∵360<400,∴够用.


科目:初中数学 来源: 题型:
【题目】长城科技公司生产销售一种电子产品,该产品总成本包括技术成本、制造成本、销售成本三部分,经核算,![]() 年该产品各部分成本所占比例约为
年该产品各部分成本所占比例约为![]() .且
.且![]() 年该产品的技术成本、制造成本分别为
年该产品的技术成本、制造成本分别为![]() 万元、
万元、![]() 万元.
万元.
![]() 确定
确定![]() 的值,并求
的值,并求![]() 年产品总成本为多少万元;
年产品总成本为多少万元;
![]() 为降低总成本,该公司
为降低总成本,该公司![]() 年及
年及![]() 年增加了技术成本投入,确保这两年技术成本都比前一年增加一个相同的百分数
年增加了技术成本投入,确保这两年技术成本都比前一年增加一个相同的百分数![]() ,制造成本在这两年里都比前一年减少一个相同的百分数
,制造成本在这两年里都比前一年减少一个相同的百分数![]() ;同时为了扩大销售量,
;同时为了扩大销售量,![]() 年的销售成本将在
年的销售成本将在![]() 年的基础上提高
年的基础上提高![]() ,经过以上变革,预计
,经过以上变革,预计![]() 年该产品总成本达到
年该产品总成本达到![]() 年该产品总成本的
年该产品总成本的![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与应用:
一个西瓜放在桌子上用刀切下去,一刀可以切成2块,2刀最多可以切成4块;3刀最多可以切成7块,4刀最多可以切成11块(如图).

上述问题转化为数学模型实际上就是n条直线最多把平面分成几块的问题,有没有规律呢?请先进行试验,然后回答以下问题.
(1)填表:

(2)设n条直线把平面最多分成的块数是S,请写出S关于n的表达式.(不需要解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,弦AB、CD互相垂直,垂足为E,点M在CD上,连接AM并延长交BC于点F,交圆上于点G,连接AD,AD=AM.
(1)如图1,求证:AG⊥BC;
(2)如图2,连接EF,DG,求证:EF∥DG;
(3)如图3,在(2)的条件下,连接BG,若∠ABG=2∠BAG,EF=15,AB=32,求BG长.

查看答案和解析>>
科目:初中数学 来源: 题型:
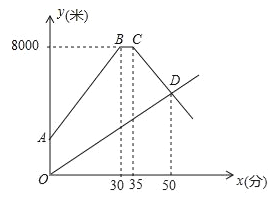
【题目】甲乙两地相距8000米.张亮骑自行车从甲地出发匀速前往乙地,出发10分钟后,李伟步行从甲地出发同路匀速前往乙地.张亮到达乙地后休息片刻,以原来的速度从原路返回.如图所示是两人离甲地的距离y(米)与李伟步行时间x(分)之间的函数图象.
(1)求两人相遇时李伟离乙地的距离;
(2)请你判断:当张亮返回到甲地时,李伟是否到达乙地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分) “先学后教”课题组对学生参与小组合作的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.课题组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了______名学生;
(2)请将条形统计图补充完整;
(3)求出扇形统计图中,“主动质疑”所对应扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
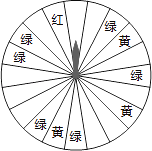
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=AB,B1C=BC,C1A=CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1A1至A2,B2,C2,使得A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,记其面积为S2…,按此规律继续下去.第n次操作得到△AnBnn,则S1=_____,△AnBnn的面积Sn=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com