Question

【题目】在平面直角坐标系中，抛物线经过两点．

（1）求此抛物线的解析式；

（2）设抛物线的顶点为，将直线沿轴向下平移两个单位得到直线，直线与抛物线的对称轴交于点，求直线的解析式；

（3）在（2）的条件下，求到直线距离相等的点的坐标．

Answer 1

【答案】（1）y=（2）y=x（3）M（，0）、A（0，2）、（0，-2）、（，0）

【解析】

试题（1）把坐标代入抛物线解析式即可．
（2）先设出平移后的直线的解析式，然后根据（1）的抛物线的解析式求出点的坐标，然后将点的坐标代入直线中即可得出直线的解析式．
（3）本题关键是找出所求点的位置，根据此点到直线的距离都相等，因此这类点应该有4个，均在的内角平分线上（外有3个，三条角平分线的交点是一个），可据此来求此点的坐标．

试题解析：(1)根据题意得

解得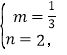

所以抛物线的解析式为：

(2)由得抛物线的顶点坐标为

依题意,可得 且直线过原点，

设直线的解析式为y=kx,则

解得

所以直线l的解析式为

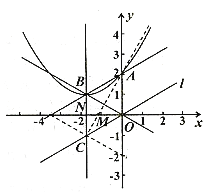
(3)到直线OB、OC、BC距离相等的点有四个，如图，

由勾股定理得OB=OC=BC=2，所以△OBC为等边三角形.

易证x轴所在的直线平分∠BOC，y轴是△OBC的一个外角的平分线，

作∠BCO的平分线,交x轴于点,交y轴于点，

作△OBC的∠BCO相邻外角的角平分线,交y轴于 点，

反向延长线交x轴于 点,可得点就是到直线OB、OC、BC距离相等的点.

可证均为等边三角形，可求得：

① 所以点的坐标为

②点与点A重合,所以点的坐标为(0,2)，

③点 与点A关于x轴对称,所以点的坐标为(0,2)，

④设抛物线的对称轴与x轴的交点为N，

且

所以点的坐标为

综合所述，到直线OB、OC、BC距离相等的点的坐标分别为：