
【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如下表格:
的图象可以得到如下表格:
|
|
|
|
|
|
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可得到如下表格:
的图象可得到如下表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() 的图象;
的图象;
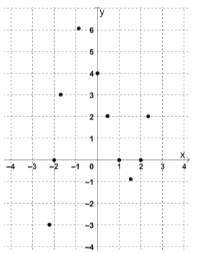
观察函数![]() 的图象,
的图象,
补全下面的表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法,解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
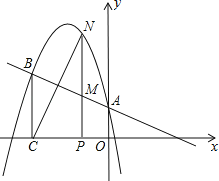
【题目】二次函数y=﹣![]() x2+bx+c的图象与直线y=﹣
x2+bx+c的图象与直线y=﹣![]() x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为C(﹣3,0).
x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为C(﹣3,0).
(1)填空:b=_____,c=_____.
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过B作BE![]() AC,与BD的垂线DE交于点E,
AC,与BD的垂线DE交于点E,
(1)求证:△ABC≌△BDE
(2)三角形BDE可由三角形ABC旋转得到,利用尺规作出旋转中心O(保留作图痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电生产厂家去年销往农村的某品牌洗碗机每台的售价![]() (元)与月份
(元)与月份![]() 之间满足函数关系
之间满足函数关系![]() ,去年的月销售量户(万台)与月份
,去年的月销售量户(万台)与月份![]() 之间成一次函数关系,其中两个月的销售情况如表:
之间成一次函数关系,其中两个月的销售情况如表:
月份: | 1月 | 5月 |
销售量: | 3.9万台 | 4.3万台 |
(1)求该品牌洗碗机在去年哪个月销往农村的销售金额最大?最大是多少?(提示:销售金额=销量×售价)
(2)经统计和计算.得到此洗碗机在农村地区的销售数据,如表:
销售数据信息表 | 售价(元/台) | 销量(万台) | 补贴金额(万元) |
去年12月份 | 2000 | 5 | / |
今年2月份 |
|
| / |
今年3月份 |
|
| 312 |
由于国家实施“家电下乡政策”,所以今年3月份国家按该产品售价的13%给子财政补贴,共补贴了312万元,从表格中,我们可以看出:今年3月份与今年2月份相比较,售价保持不变,但销量增加了1.5万台.今年2月份与去年12月份相比较,售价下降了![]() %,销量下降了1.5
%,销量下降了1.5![]() %;请用
%;请用![]() 表示表格中的
表示表格中的![]() ,
,![]() ,并根据已知条件求出
,并根据已知条件求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点在原点![]() ,对称轴为
,对称轴为![]() 轴.一次函数
轴.一次函数![]() 的图象与二次函数的图象交于
的图象与二次函数的图象交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的左侧),且
的左侧),且![]() 点坐标为
点坐标为![]() .平行于
.平行于![]() 轴的直线
轴的直线![]() 过
过![]() 点.
点.
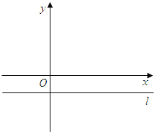
![]() 求一次函数与二次函数的解析式;
求一次函数与二次函数的解析式;
![]() 判断以线段
判断以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并给出证明;
的位置关系,并给出证明;
![]() 把二次函数的图象向右平移
把二次函数的图象向右平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位
个单位![]() ,二次函数的图象与
,二次函数的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,一次函数图象交
两点,一次函数图象交![]() 轴于
轴于![]() 点.当
点.当![]() 为何值时,过
为何值时,过![]() ,
,![]() ,
,![]() 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为![]() 的直径,C、D为
的直径,C、D为![]() 上两点,且
上两点,且![]() ,垂足为F,直线CF交AB的延长线于点E,连接AC
,垂足为F,直线CF交AB的延长线于点E,连接AC
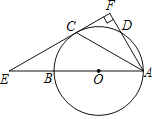
(1)判断EF与![]() 的位置关系,并说明理由:
的位置关系,并说明理由:
(2)若![]() ,
,![]() 的半径为4,求线段CF的长.
的半径为4,求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
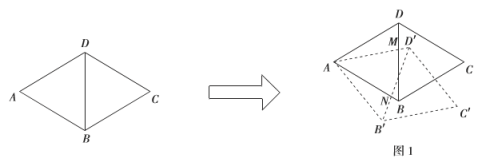
问题情境:在一次综合实践活动课上,同学们以菱形为对象,研究菱形旋转中的问题:已知,在菱形![]() 中,
中, ![]() 为对角线,
为对角线, ![]() ,
,![]() ,将菱形
,将菱形![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() (单位
(单位![]() ),旋转后的菱形为
),旋转后的菱形为![]() ,在旋转探究活动中提出下列问题,请你帮他们解决.
,在旋转探究活动中提出下列问题,请你帮他们解决.
观察证明:
(1)如图1,若旋转角![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,请说明线段
,请说明线段![]() 与
与![]() 的数量关系;
的数量关系;
操作计算:
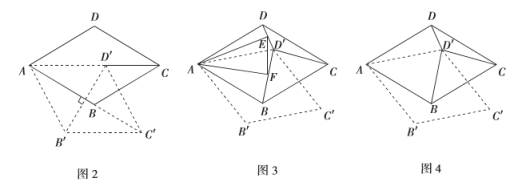
(2)如图2,连接![]() ,菱形
,菱形![]() 旋转的过程中,当
旋转的过程中,当![]() 与
与![]() 互相垂直时,
互相垂直时, ![]() 的长为 ;
的长为 ;
(3)如图3,若旋转角![]() ,分别连接
,分别连接![]() ,
,![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() ,连接
,连接![]() ,菱形
,菱形![]() 旋转的过程中,发现在
旋转的过程中,发现在![]() 中存在长度不变的线段
中存在长度不变的线段![]() ,请求出
,请求出![]() 长度;
长度;
操作探究:
(4)如图4,在(3)的条件下,请判断以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是什么特殊三角形,并说明理由.
三条线段长度为边的三角形是什么特殊三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价y1(元/台)与采购数量x1(台)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).
(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的![]() ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?
(2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com