
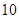 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产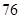 件,每件利润
件,每件利润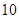 元,每提高一个档次,利润每件增加
元,每提高一个档次,利润每件增加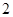 元.
元. 元时,此产品质量在第几档次?
元时,此产品质量在第几档次? 件.若生产第
件.若生产第 档的产品一天的总利润为
档的产品一天的总利润为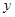 元(其中
元(其中 为正整数,且
为正整数,且 ≤
≤ ≤
≤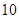 ),求出
),求出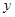 关于
关于 的函数关系式;若生产某档次产品一天的总利润为
的函数关系式;若生产某档次产品一天的总利润为 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品? 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源:不详 题型:解答题
 经过点B(
经过点B( ,2),且与x轴交于点A.将抛物线
,2),且与x轴交于点A.将抛物线 沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
 平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.
平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,下列说法错误的是( )
,下列说法错误的是( )A.当 时, 时, 随 随 的增大而减小 的增大而减小 |
B.若图象与 轴有交点,则 轴有交点,则 |
C.当 时,不等式 时,不等式 的解集是 的解集是 |
D.若将图象向上平移1个单位,再向左平移3个单位后过点 ,则 ,则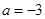 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且
与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 间,当每间客房的定价为每天
间,当每间客房的定价为每天 元时,客房会全部住满.当每间客房每天的定价每涨
元时,客房会全部住满.当每间客房每天的定价每涨 元时,就会有
元时,就会有 间客房空闲.如果旅客居住客房,宾馆需对每间客房每天支出
间客房空闲.如果旅客居住客房,宾馆需对每间客房每天支出 元的各种费用.
元的各种费用. (元)与每间客房涨价
(元)与每间客房涨价 (元)之间的函数关系式;
(元)之间的函数关系式; 元,
元, 元的利润是否为该天的最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时客房定价应为多少元?
元的利润是否为该天的最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时客房定价应为多少元?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
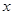 轴交于点
轴交于点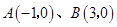 两点,与
两点,与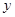 轴交于点
轴交于点 以
以 为直径作
为直径作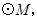 过抛物线上一点
过抛物线上一点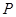 作
作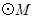 的切线
的切线 切点为
切点为 并与
并与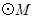 的切线
的切线 相交于点
相交于点 连结
连结 并延长交
并延长交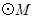 于点
于点 连结
连结

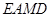 的面积为
的面积为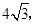 求直线
求直线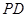 的函数关系式;
的函数关系式;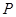 ,使得四边形
,使得四边形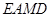 的面积等于
的面积等于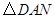 的面积?若存在,求出点
的面积?若存在,求出点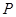 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由. 查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.a>0,b<0,c>0 | B.a<0,b<0,c>0 |
| C.a<0,b>0,c<0 | D.a<0,b>0,c>0 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com