
【题目】如图,已知□ABCD的对角线AC , BD相交于点O , 直线EF经过点O , 且分别交AB , CD于点E , F.求证:四边形BFDE是平行四边形..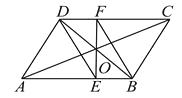

【答案】证明:∵□ABCD的对角线AC , BD相交于点O ,
∴OA=OC , OB=OD , ∠DCO=∠BAO
又∵∠AOE=∠COD,
∴△AOE≌△COF ,
得OE=OF ,
∴四边形BFDE是平行四边形.
【解析】由平行四边形的性质得到OA=OC , OB=OD , ∠DCO=∠BAO , 再由ASA证得△AOE≌△COF , 可推出OE=OF , 从而得到对角线互相平分的四边形是平行四边形.
【考点精析】根据题目的已知条件,利用平行四边形的判定的相关知识可以得到问题的答案,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】小明的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC , BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( ) 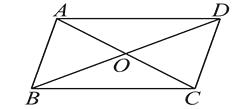
A.对角线互相平分的四边形是平行四边形,
B.两组对角分别相等的四边形是平行四边形,
C.两组对边分别平行的四边形是平行四边形,
D.两组对边分别相等的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC和BD相交于点O , E , F分别为OB , OD的中点,过点O任作一直线分别交AB , CD于点G , H.
试说明:GF∥EH.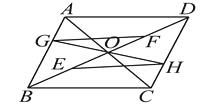

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com