
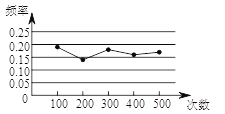
【题目】某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
A. 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球
B. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
C. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
【答案】B
【解析】根据附近统计图可知,试验结果在0.16波动,即其概率P≈0.16,计算四个选项的概率,约为0.16者即为正确答案.
解:A、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率为![]() ,故本选项错误;
,故本选项错误;
B、袋子中有一个红球和2个黄球,只有颜色上的区别,从中随机地取出一个球是黄球的概率为![]() ,故本选项错误;
,故本选项错误;
C、掷一枚质地均匀的硬币,落地时结果是“正面向上”的概率是![]() ,故本选项错误;
,故本选项错误;
D、掷一枚质地均匀的正六边体骰子,落地时面朝上的点数是6的概率为![]() ≈0.17,故本选项正确.
≈0.17,故本选项正确.
故选D.
“点睛”本题考查了利用频率估算概率,大量反复试验下频率稳定值即概率,用到的知识点为:概率=所求情况数与总情况数之比. 同时此题在解答中要用到概率公式.


科目:初中数学 来源: 题型:
【题目】为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
组别 | 捐款额(x)元 | 户数 |
A | 1≤x<50 | a |
B | 50≤x<100 | 10 |
C | 100≤x<150 | |
D | 150≤x<200 | |
E | x≥200 |
请结合以上信息解答下列问题.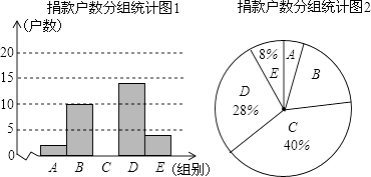
(1)a= , 本次调查样本的容量是;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料360kg,乙种原料290kg,计划用这两种原料生产A、B两种产品共50件,已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg,可获利润700元;生产一件B种产品,需用甲种原料4kg,乙种原料10kg,可获利润1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润是W(元),采用哪种生产方案获总利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x1 , x2 , x3 , x4 , x5 , x6 , x7是自然数,且x1<x2<x3<x4<x5<x6<x7 , x1+x2=x3 , x2+x3=x4 , x3+x4=x5 , x4+x5=x6 , x5+x6=x7 , 又x1+x2+x3+x4+x5+x6+x7=2010,那么x1+x2+x3的值最大是。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算过程中有错误的个数是( )![]() ;
;
(2)﹣4×(﹣7)×(﹣125)=﹣(4×125×7);![]() ;
;
(4)[3×(﹣2)]×(﹣5)=3×2×5.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com