
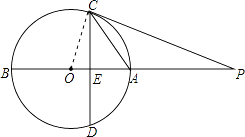
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PEPO.
(1)求证:PC是⊙O的切线.
(2)若OE:EA=1:2,PA=6,求⊙O的半径.
【答案】
(1)证明:连结OC,如图,
∵CD⊥AB,
∴∠PEC=90°,
∵PC2=PEPO,
∴PC:PO=PE:PC,
而∠CPE=∠OPC,
∴△PCE∽△POC,
∴∠PEC=∠PCO=90°,
∴OC⊥PC,
∴PC是⊙O的切线
(2)解:设OE=x,则EA=2x,OA=OC=3x,
∵∠COE=∠POC,∠OEC=∠OCP,
∴△OCE∽△OPC,
∴OC:OP=OE:OC,即3x:OP=x:3x,解得OP=9x,
∴3x+6=9x,解得x=1,
∴OC=3,
即⊙O的半径为3.
【解析】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.也考查了切线的判定方法.(1)连结OC,如图,由PC2=PEPO和公共角可判断△PCE∽△POC,则∠PEC=∠PCO=90°,然后根据切线的判定定理可判断PC是⊙O的切线;(2)设OE=x,则EA=2x,OA=OC=3x,证明△OCE∽△OPC,利用相似比可表示出OP,则可列方程3x+6=9x,然后解出x即可得到⊙O的半径.
【考点精析】根据题目的已知条件,利用垂径定理和切线的判定定理的相关知识可以得到问题的答案,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


科目:初中数学 来源: 题型:
【题目】书店举行购书优惠活动:
①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元一律打九折;
③一次性购书超过200元一律打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是博文学校初三一班慧慧、聪聪两名学生入学以来10次数学检测成绩(单位:分).
慧慧 | 116 | 124 | 130 | 126 | 121 | 127 | 126 | 122 | 125 | 123 |
聪聪 | 122 | 124 | 125 | 128 | 119 | 120 | 121 | 128 | 114 | 119 |
回答下列问题:
(1)分别求出慧慧和聪聪成绩的平均数;
(2)分别计算慧慧和聪聪两组数据的方差;
(3)根据(1)(2)你认为选谁参加全国数学竞赛更合适?并说明理由;
(4)由于初三二班、初三三班和初三四班数学成绩相对薄弱,学校打算派慧慧和聪聪分别参加三个班的数学业余辅导活动,求两名学生分别在初三二班和初三三班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,P为边AB上一点.
(1)如图1,若∠ACP=∠B,求证:AC2=APAB;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB= ![]() ,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=( )
,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程x2﹣3x+p=0(p≠0)的两个不相等的实数根分别为a和b,且a2﹣ab+b2=18,则 ![]() +
+ ![]() 的值是( )
的值是( )
A.3
B.﹣3
C.5
D.﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: ![]() =
= ![]() ;
;
【结论应用】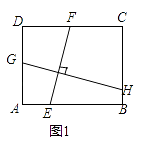
(2)如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 ![]() =
= ![]() ,则
,则 ![]() 的值为;
的值为;
【联系拓展】
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求 ![]() 的值.
的值.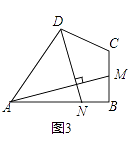
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣4ax+b与x轴的一个交点A的坐标为(3,0),与y轴交于点C.
(1)求抛物线与x轴的另一个交点B的坐标;
(2)当a=﹣1时,将抛物线向上平移m个单位后经过点(5,﹣7).
①求m的值及平移前、后抛物线的顶点P、Q的坐标.
②设平移后抛物线与y轴交于点D,问:在平移后的抛物线上是否存在点E,使得△ECD的面积是△EPQ的3倍?若存在,请求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com