
【题目】如图,已知直线y=x+5与x轴交于点A,直线y=kx+b与x轴交于点B(1,0),且与直线y=x+5交于第二象限点C(m,n).
(1)若△ABC的面积为12,求点C的坐标及关于x的不等式的x+5>kx+b解集;
(2)求k的取值范围.

【答案】(1)x>﹣1;(2)﹣5<k<0.
【解析】
1)由题意可求点A坐标,由三角形面积关系可求点C坐标,由一次函数性质可求不等式解集;
(2)列出方程组,用参数k表示点C坐标,由点C坐标在第二象限列出不等式组可求k的取值范围.
解:(1)∵直线y=x+5与x轴交于点A
∴x+5=0 解得:x=﹣5
∴A(﹣5,0)
∵B(1,0)
∴AB=1﹣(﹣5)=6
∵C(m,n)
∵S△ABC=![]() AByC=
AByC=![]() ×6n=3n=12
×6n=3n=12
∴n=4
∵点C(m,n)在直线AB上
∴m+5=n=4
∴m=﹣1
∴点C坐标为(﹣1,4)
由图象可知,不等式x+5>kx+b的解集为x>﹣1.
(2)∵直线y=kx+b与x轴交于点B(1,0),
∴0=k+b
∴b=﹣k
∴y=kx﹣k
∵直线y=kx+b与x轴交于点B(1,0),且与直线y=x+5交于第二象限点C(m,n).
∴![]()
∴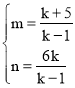
∵m<0,n>0
∴﹣5<k<0


科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=___________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>1时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线L与y=2x+1的交于点A(2,a),与直线y=x+2的交于点B(b,1)
(1)求a,b的值;
(2)求直线l的函数表达式;
(3)求直线L、x轴、直线y=2x+1围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,万州区某中学举行了一次中学生诗词大赛活动.小何同学对他所在八年级一班参加诗词大赛活动同学的成绩进行了整理,成绩分别100分、90分、80分、70分,并绘制出如下的统计图.
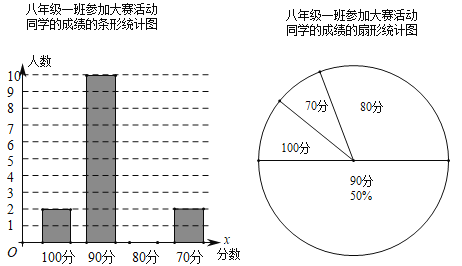
请根据以上提供的信息,解答下列问题:
(1)该校八年级(1)班参加诗词大赛成绩的众数为______分;并补全条形统计图.
(2)求该校八年级(1)班参加诗词大赛同学成绩的平均数;
(3)结合平时成绩、期中成绩和班级预选成绩(如下表),年级拟从该班小何和小王的两位同学中选一名学生参加区级决赛,按![]() 的比例计算两位同学的最终得分,请你根据计算结果确定选谁参加区级决赛.
的比例计算两位同学的最终得分,请你根据计算结果确定选谁参加区级决赛.
学生姓名 | 平时成绩 | 期中成绩 | 预选成绩 |
小何 | 80 | 90 | 100 |
小王 | 90 | 100 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B,C在数轴上表示数a,b,c,满足(b+2)2+(c﹣24)2=0,多项式x|a+3|y2﹣ax3y+xy2﹣1是关于字母x,y的五次多项式.
(1)a的值________,b的值________,c的值________.
(2)已知蚂蚁从A点出发,途径B,C两点,以每秒3cm的速度爬行,需要多长时间到达终点C?
(3)求值:a2b﹣bc.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校假期由校长带领该校“三好学生”去旅游,甲旅行社说“若校长买全票一张,则学生半价.”乙旅行社说“全部人六折优惠”若全票价是1200元,则:
(1)若学生人数是20人,甲、乙旅行社收费分别是多少?
(2)当学生人数的多少时,两家旅行社的收费一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句正确的个数是( )
①收入增加100元与支出减少200元是一对具有相反意义的量;
②数轴上原点两侧的数互为相反数;
③若一个数小于他的绝对值,则这个数是负数;
④若a、b互为相反数,则![]() 与
与![]() 也互为相反数
也互为相反数
A.1个B.2个C.3个D.0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com