
分析 (1)由M-N是一个完全平方式,分解因式得出M-N=(a-b)2≥0,即可得出结论;
(2)由(1)的结论容易得出结果;
(3)把原式化成=$\frac{1}{2}$[(a-b)2+(a-c)2+(b-c)2],即可得出结论.
解答 解:(1)M≥N;理由如下:
∵M-N=a2+b2-2ab=(a-b)2≥0,∴M≥N;
(2)∵$\frac{y^2}{x^2}+\frac{x^2}{y^2}+3$$≥2×\frac{y}{x}×\frac{x}{y}+3=5$
∴最小值为5;
(3)a2+b2+c2-ab-ac-bc>0,理由如下:
∵a2+b2+c2-ab-ac-bc
=$\frac{1}{2}$(2a2+2b2+2c2-2ab-2ac-2bc)
=$\frac{1}{2}$[(a-b)2+(a-c)2+(b-c)2],
∵a,b,c为互不相等的实数,
∴a2+b2+c2-ab-ac-bc>0.
点评 本题考查了因式分解的应用、偶次方的非负性质;熟练掌握用完全平方公式分解因式,并能进行推理论证是解决问题的关键.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:填空题
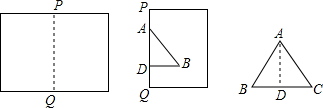
 如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.
如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
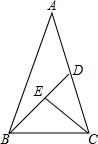 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E.设k=$\frac{\sqrt{5}-1}{2}$,则DE=$\frac{3-\sqrt{5}}{2}$a.
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E.设k=$\frac{\sqrt{5}-1}{2}$,则DE=$\frac{3-\sqrt{5}}{2}$a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
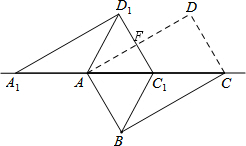 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分面积为S,则下列结论:
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分面积为S,则下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com