
【题目】如图,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有( ) 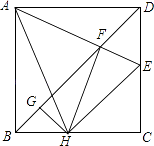
A.①②③
B.①②④
C.①③④
D.①②③④
【答案】D
【解析】
解答:解:①连接FC,延长HF交AD于点L,
∵BD为正方形ABCD的对角线,
∴∠ADB=∠CDF=45°.
∵AD=CD,DF=DF,
∴△ADF≌△CDF.
∴FC=AF,∠ECF=∠DAF.
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°.
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC.
∴FH=AF.
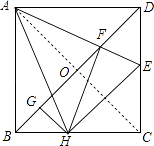
②∵FH⊥AE,FH=AF,
∴∠HAE=45°.
③连接AC交BD于点O,可知:BD=2OA,
∵∠AFO+∠GFH=∠GHF+∠GFH,
∴∠AFO=∠GHF.
∵AF=HF,∠AOF=∠FGH=90°,
∴△AOF≌△FGH.
∴OA=GF.
∵BD=2OA,
∴BD=2FG.
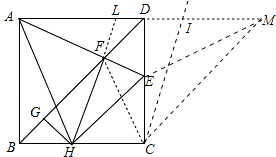
④延长AD至点M,使AD=DM,过点C作CI∥HL,则:LI=HC,
根据△MEC≌△MIC,可得:CE=IM,
同理,可得:AL=HE,
∴HE+HC+EC=AL+LI+IM=AM=8.
∴△CEM的周长为8,为定值.
故(1)(2)(3)(4)结论都正确.
故选D.
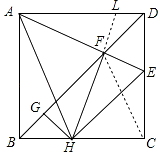
分析:①作辅助线,延长HF交AD于点L,连接CF,通过证明△ADF≌△CDF,可得:AF=CF,故需证明FC=FH,可证:AF=FH;
②由FH⊥AE,AF=FH,可得:∠HAE=45°;
③作辅助线,连接AC交BD于点O,证BD=2FG,只需证OA=GF即可,根据△AOF≌△FGH,可证OA=GF,故可证BD=2FG;(4)作辅助线,延长AD至点M,使AD=DM,过点C作CI∥HL,则IL=HC,可证AL=HE,再根据△MEC≌△MIC,可证:CI=IM,故△CEM的周长为边AM的长,为定值
解答本题要充分利用正方形的特殊性质,在解题过程中要多次利用三角形全等


科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边三角形ACD及等边三角形ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证: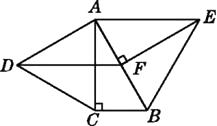
(1)AC=EF;
(2)四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
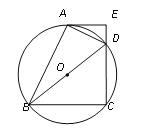
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的口袋中,有三张形状、大小、质地完全相同的纸片,三张纸片上分别写有函数:①y=﹣x,②y=﹣![]() ,③y=2x2.
,③y=2x2.
(1)在上面三个函数中,其函数图象满足在第二象限内y随x的增大而减小的函数有 (请填写序号);现从口袋中随机抽取一张卡片,则抽到的卡片上的函数图象满足在第二象限内y随x的增大而减小的概率为 ;
(2)王亮和李明两名同学设计了一个游戏,规则为:王亮先从口袋中随机抽取一张卡片,不放回,李明再从口袋中随机抽取一张卡片,若两人抽到的卡片上的函数图象都满足在第二象限内y随x的增大而减小,则王亮得3分,否则李明得2分,请用列表或画树状图的方法说明这个游戏对双方公平吗?若你认为不公平,如何修改规则才能使该游戏对双方公平呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
这些数据说明:植物每天高度增长量![]() 关于温度
关于温度![]() 的函数是反比例函数、一次函数和二次函数中的一种.
的函数是反比例函数、一次函数和二次函数中的一种.
(1)你认为是哪一种函数,并求出它的函数关系式;
(2)温度为多少时,这种植物每天高度增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度![]() 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com