
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边三角形ACD及等边三角形ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证: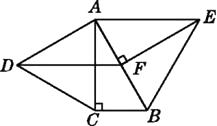
(1)AC=EF;
(2)四边形ADFE是平行四边形.
【答案】
(1)证明:∵在Rt△ABC中,∠BAC=30°,
∴BC= ![]() AB.
AB.
∵△ABE是等边三角形,EF⊥AB,
∴AB=EB,BF= ![]() AB.
AB.
∴BC=BF.
在Rt△ACB和Rt△EFB中, ![]()
∴Rt△ACB≌Rt△EFB(HL).∴AC=EF.
(2)证明:∵△ADC是等边三角形,∴∠DAC=60°,AC=AD.
∴AD=EF.∵∠BAC=30°,
∴∠DAF=∠DAC+∠BAC=90°.
∴∠DAF=∠AFE.∴AD∥EF.
∴四边形ADFE是平行四边形
【解析】(1)根据30°角所对的的直角边等于斜边的一半证出BC=![]() AB,再根据等边三角形的性质证明BF=
AB,再根据等边三角形的性质证明BF=![]() AB,得到BC=BF,然后根据直角三角形的全等判定证明Rt△ACB≌Rt△EFB,再根据全等三角形的性质就可证得结论。
AB,得到BC=BF,然后根据直角三角形的全等判定证明Rt△ACB≌Rt△EFB,再根据全等三角形的性质就可证得结论。
(2)根据已知易证AD=EF,再根据等边三角形的性质证明∠DAC=60°及∠DAC=60°,可证得∠DAF=∠AFE=90°,就可证得AD∥EF,然后根据平行四边形的判定即可证得结论。


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i.
(2)求DC的长.(参考数据:sin73.5°≈0.96,con73.5°≈0.28,tan73.5°≈3.4, ![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于多项式x2+y2-1的项数及次数,下列说法正确的是( )
A.项数是2,次数是2B.项数是2,次数是4
C.项数是3,次数是2D.项数是3,次数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.求证: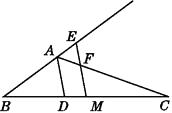
(1)AE=AF;
(2)BE= ![]() (AB+AC).
(AB+AC).
查看答案和解析>>
科目:初中数学 来源: 题型:
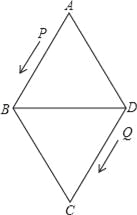
【题目】如图,菱形ABCD的边长为24厘米,∠A=60°,点P从点A出发沿线路AB→BD作匀速运动,点Q从点D同时出发沿线路DC→CB→BA作匀速运动.
(1)求BD的长;
(2)已知点P、Q运动的速度分别为4厘米/秒,5厘米/秒,经过12秒后,P、Q分别到达M、N两点,若按角的大小进行分类,请你确定△AMN是哪一类三角形,并说明理由;
(3)设(2)中的点P、Q分别从M、N同时沿原路返回,点P的速度不变,点Q的速度改变为a厘米/秒,经过3秒后,P、Q分别到达E、F两点,若△BEF与(2)中的△AMN相似,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,E为CD上一动点,AE交BD于F,过F作FH⊥AE于H,过H作GH⊥BD于G,下列有四个结论:①AF=FH,②∠HAE=45°,③BD=2FG,④△CEH的周长为定值,其中正确的结论有( ) 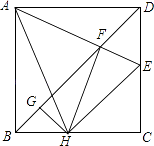
A.①②③
B.①②④
C.①③④
D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com