
【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.求证: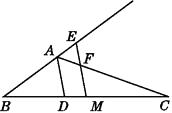
(1)AE=AF;
(2)BE= ![]() (AB+AC).
(AB+AC).
【答案】
(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵AD∥EM,
∴∠BAD=∠AEF,∠CAD=∠AFE.
∴∠AEF=∠AFE.
∴AE=AF.
(2)证明:如图,在BE的延长线上截取EG=BE,并连接CG.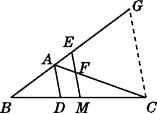
∵BM=CM,∴EM为△BCG的中位线.
∴EM∥CG.∴∠AGC=∠AEF,∠ACG=∠AFE.
∵∠AEF=∠AFE,
∴∠AGC=∠ACG.
∴AG=AC.
∴BE= ![]() BG=
BG= ![]() (AB+AG)=
(AB+AG)= ![]() (AB+AC)
(AB+AC)
【解析】(1)根据角平分线的定义得出∠BAD=∠CAD,再根据平行线的性质得出∠BAD=∠AEF,∠CAD=∠AFE,就可证得∠AEF=∠AFE,然后根据等边对等角即可证得结论。
(2)在BE的延长线上截取EG=BE,并连接CG,构造△ACG的中位线得出EM∥CG,根据平行线的性质证得∠AGC=∠AEF,∠ACG=∠AFE,再根据∠AEF=∠AFE,从而得到∠AGC=∠ACG,根据等角对等边证出AG=AC,然后根据BE= ![]() BG,就可证得结论。
BG,就可证得结论。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点D,E,F分别为△ABC各边的中点,下列说法正确的是( )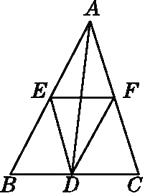
A.DE=DF
B.EF= ![]() AB
AB
C.S△ABD=S△ACD
D.AD平分∠BAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为C1,把锅盖纵断面的抛物线记为C2.
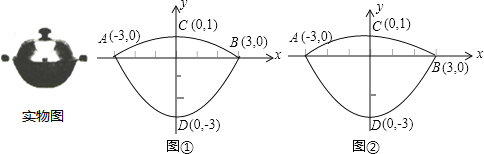
(1)求C1和C2的解析式;
(2)如果炒菜时锅的水位高度是1dm,求此时水面的直径;
(3)如果将一个底面直径为3dm,高度为3dm的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E,F分别在AD,BC上,若要使四边形AFCE是平行四边形,可以添加的条件是( )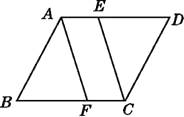
①AF=CF;②AE=CE;③BF=DE;④AF∥CE.
A.①或②
B.②或③
C.③或④
D.①或③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边三角形ACD及等边三角形ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证: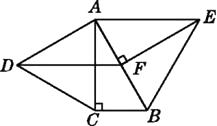
(1)AC=EF;
(2)四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
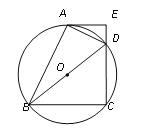
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com