
【题目】在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连接BD,CD,其中CD交直线AP于点E.
(1)依题意补全图1;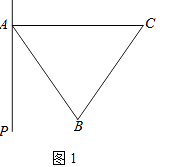
(2)若∠PAB=30°,求∠ACE的度数;
(3)如图2,若60°<∠PAB<120°,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并证明.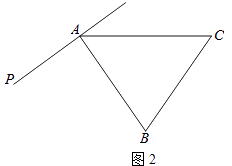
【答案】
(1)
解:所作图形如图1所示:
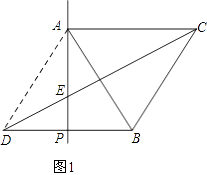
(2)
解:连接AD,如图1.
∵点D与点B关于直线AP对称,
∴AD=AB,∠DAP=∠BAP=30°,
∵AB=AC,∠BAC=60°,
∴AD=AC,∠DAC=120°,
∴2∠ACE+60°+60°=180°,
∴∠ACE=30°

(3)
解:线段AB,CE,ED可以构成一个含有60°角的三角形.
证明:连接AD,EB,如图2.
∵点D与点B关于直线AP对称,
∴AD=AB,DE=BE,
∴∠EDA=∠EBA,
∵AB=AC,AB=AD,
∴AD=AC,
∴∠ADE=∠ACE,
∴∠ABE=∠ACE.
设AC,BE交于点F,
又∵∠AFB=∠CFE,
∴∠BAC=∠BEC=60°,
∴线段AB,CE,ED可以构成一个含有60°角的三角形.
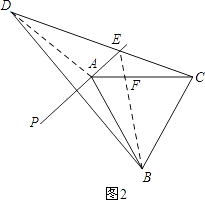
【解析】(1)根据题意作出图形;(2)根据题意可得∠DAP=∠BAP=30°,然后根据AB=AC,∠BAC=60°,得出AD=AC,∠DAC=120°,最后根据三角形的内角和公式求解;(3)由线段AB,CE,ED可以构成一个含有60度角的三角形,连接AD,EB,根据对称可得∠EDA=∠EBA,然后证得AD=AC,最后即可得出∠BAC=∠BEC=60°.


科目:初中数学 来源: 题型:
【题目】下列事件中,属于必然事件的是( )
A.掷一枚硬币,正面朝下
B.三角形两边之和大于第三边
C.一个三角形三个内角的和小于180°
D.在一个没有红球的盒子里,摸到红球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图:根据图中所给信息,全校喜欢娱乐类节目的学生大约有( )人.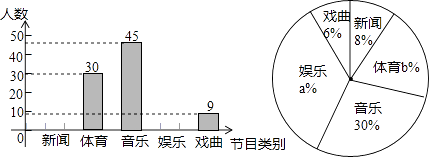
A.1080
B.900
C.600
D.108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数为:①在等圆中,等弦对等弧;②直径是圆的对称轴;③平分弦的直径垂直于这条弦;④弦的中垂线一定经过圆心.( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
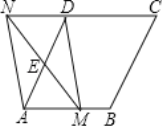
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学要证明命题“平行四边形的对边相等.”是正确的,他画出了图形,并写出了如下已知和不完整的求证.
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,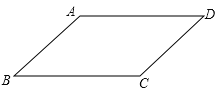
(1)补全求证部分;
(2)请你写出证明过程.
证明: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com