
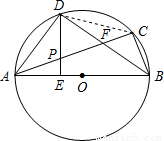
(本题满分12分)已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.

(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD=3,BD=4,求⊙O的半径和DE的长.
(1)证明见试题解析;(2)证明见试题解析;(3)2.5,2.4.
【解析】
试题分析:(1)利用角平分线的性质得出∠CBD=∠DBA,进而得出∠DAC=∠DBA,再利用互余的性质得出∠DAC=∠ADE,进而得出∠DAC=∠DBA;
(2)利用圆周角定理得出∠ADB=90°,进而求出∠PDF=∠PFD,则PD=PF,求出PA=PF,即可得出答案;
(3)利用勾股定理得出AB的长,再利用三角形面积求出DE即可.
试题解析:(1)∵BD平分∠CBA,∴∠CBD=∠DBA,
∵∠DAC与∠CBD都是弧CD所对的圆周角,∴∠DAC=∠CBD,∴∠DAC=∠DBA,
∵AB是⊙O的直径,DE⊥AB,∴∠ADB=∠AED=90°,∴∠ADE+∠DAE=90°,∠DBA+∠DAE=90°,
∴∠ADE=∠DBA,∴∠DAC=∠ADE,∴∠DAC=∠DBA;
(2)证明:∵AB为直径,∴∠ADB=90°,
∵DE⊥AB于E,∴∠DEB=90°,∴∠ADE+∠EDB=∠ABD+∠EDB=90°,∴∠ADE=∠ABD=∠DAP,
∴PD=PA,
∵∠DFA+∠DAC=∠ADE+∠PDF=90°,且∠ADB=90°,∴∠PDF=∠PFD,∴PD=PF,∴PA=PF,即P是线段AF的中点;
(3)【解析】
连接CD,
∵∠CBD=∠DBA,∴CD=AD,
∵CD﹦3,∴AD=3,∵∠ADB=90°,∴AB=5,故⊙O的半径为2.5,
∵DE×AB=AD×BD,∴5DE=3×4,∴DE=2.4.即DE的长为2.4.
考点:圆的综合题.


科目:初中数学 来源:2014-2015学年江苏省江阴市华士片九年级上学期期中考试数学试卷(解析版) 题型:选择题
方程 的解是( )
的解是( )
A.x=2 B.x1=2,x2=0 C.x1= ,x2=0 D.x=0
,x2=0 D.x=0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市华士片七年级上学期期中考试数学试卷(解析版) 题型:选择题
在式子 ,
, ,0,
,0, ,
, ,
, 中,单项式的个数是( )
中,单项式的个数是( )
A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江都市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)某联欢会上有一个有奖游戏,规则如下:有3张纸牌,背面都是喜羊羊头像,正面有1张是笑脸,其余2张是哭脸.现将3张纸牌洗匀后背面朝上摆放到桌上,若翻到的纸牌中有笑脸就有奖,没有笑脸就没有奖.
(1)小芳获得一次翻牌机会,她从中随机翻开一张纸牌.小芳得奖的概率是 .
(2)小明获得两次翻牌机会,他同时翻开两张纸牌.小明认为他得奖的概率是小芳的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江都市九年级上学期期中考试数学试卷(解析版) 题型:填空题
对于实数 ,定义运算“*”:
,定义运算“*”: ,例如:
,例如: ,因为
,因为 ,所以
,所以 .若
.若 是一元二次方程
是一元二次方程 的两个根,那么
的两个根,那么 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中联考数学试卷(解析版) 题型:解答题
(1)学完全等三角形以后,老师布置了这样一道题:如图1,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q.试说明:∠BQM=60°.

(2)小丽做完后,进行了反思,提出了许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M、N分别移动到BC、CA的延长线上,是否仍能得到∠BQM=60°?
请你作出判断,在下列横线上填写“是”或“否”:① ;② .
并对②给出证明.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省七年级上学期期中联考数学试卷(解析版) 题型:填空题
在数轴上有两点A和B,已知线段AB长为4个单位,若点A表示的数是-1,则点B表示的数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com