
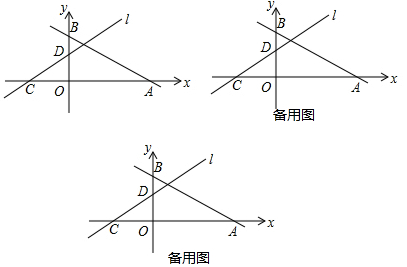
���� ��1�������B���꣬����OA=2OB���Ƴ���A���꣬��A��4��0������ֱ��y=kx+2���ɽ�����⣮
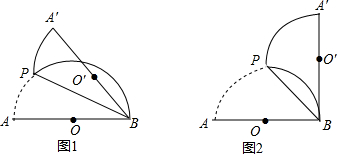
��2����ͼ1�У���P��m��$\frac{1}{2}$m+1�������������ٵ�P��AB�Ϸ�ʱ������${S}_{��{P}_{1}AB}$=${S}_{��{P}_{1}BO}$+${S}_{��{P}_{1}OA}$-S��AOB���㼴�ɣ��ڵ�P��AB�·�����C�غ�ʱ������S��AOB=$\frac{2}{3}$S��APB��
��3�����ڣ��������������ۼ��ɣ�����ͼ2�У�����AOB��ƽ���߽�CD�ڵ�M����֪M��2��2������MN��OM��x����N����MN���OA��N�䣮���OMN���ǵ���ֱ�������Σ���OMN�ǵ���ֱ�������Σ�����ͼ3�У�����M��D�غ�ʱ����x���Ͻ�ȡON=OM��ON��=OM=2����ʱ��MON���ǵ���ֱ�������Σ���MON�ǵ���ֱ�������Σ�����ͼ4�У���OMƽ�֡�BOC��CD��M����֪M��-$\frac{2}{3}$��$\frac{2}{3}$������MN��x����N����MN���OM��OC��N�䣮���OMN���ǵ���ֱ�������Σ���OMN�ǵ���ֱ�������Σ�
��� �⣺��1����ֱ��y=kx+2��y��ֱ���B�㣬
��B��0��2����
��OB=2��
��OA=2OB��
��OA=4��
��A��4��0����
��A��4��0������ֱ��y=kx+2�õ�k=-$\frac{1}{2}$��
��y=-$\frac{1}{2}$x+2��
��A��4��0����k=-$\frac{1}{2}$��
��2����ͼ1�У���P��m��$\frac{1}{2}$m+1����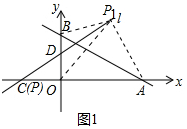
�ٵ�P��AB�Ϸ�ʱ��
��${S}_{��{P}_{1}AB}$=${S}_{��{P}_{1}BO}$+${S}_{��{P}_{1}OA}$-S��AOB��
��$\frac{2}{3}$��[$\frac{1}{2}$��2��m+$\frac{1}{2}$��4����$\frac{1}{2}$m+1��-$\frac{1}{2}$��4��2]=$\frac{1}{2}$��4��2��
���m=4����ʱ��P����Ϊ��4��3����
�ڵ�P��AB�·�����C�غ�ʱ��
����S��AOB=$\frac{2}{3}$S��APB
��ʱ��P���꣨-2��0����
��3�����ڣ��������£�
����ͼ2�У�����AOB��ƽ���߽�CD�ڵ�M����֪M��2��2������MN��OM��x����N����MN���OA��N�䣮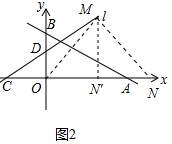
���OMN���ǵ���ֱ�������Σ�M��2��2����N�䣨2��0������OMN�ǵ���ֱ�������Σ�M��2��2����N��4��0����
����ͼ3�У�����M��D�غ�ʱ����x���Ͻ�ȡON=OM��ON��=OM=2��
��ʱ��MON���ǵ���ֱ�������Σ���ʱM��0��1����N�䣨-1��0������MON�ǵ���ֱ�������Σ���ʱM��0��1����N��1��0����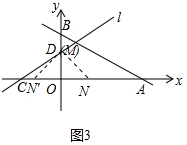
����ͼ4�У���OMƽ�֡�BOC��CD��M����֪M��-$\frac{2}{3}$��$\frac{2}{3}$������MN��x����N����MN���OM��OC��N�䣮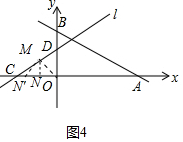
���OMN���ǵ���ֱ�������Σ�M��-$\frac{2}{3}$��$\frac{2}{3}$����N�䣨-$\frac{4}{3}$��0������OMN�ǵ���ֱ�������Σ�M��-$\frac{2}{3}$��$\frac{2}{3}$����N��-$\frac{2}{3}$��0����
���� ���⿼��һ�κ����ۺ��⡢�����ε����������ֱ�������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬��Ҫ����©�⣬ѧ���÷ָ�������ε�����������п�ѹ���⣮


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -2 | C�� | 3 | D�� | -4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
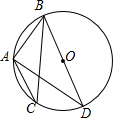 ��ͼ��BD�ǡ�O��ֱ������AB=AC����BAC=120�㣬��֪AB=2����AD=2$\sqrt{3}$��
��ͼ��BD�ǡ�O��ֱ������AB=AC����BAC=120�㣬��֪AB=2����AD=2$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
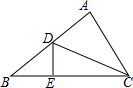 ��ͼ���ڡ�ABC�У���A=90�㣬��D��AB���ϵ�һ�㣬��D����BC�Ĵ��ߣ�����Ϊ��E����֪��AB=4cm��BC=8cm��CD=7cm�����DBE���ܳ�Ϊ��������
��ͼ���ڡ�ABC�У���A=90�㣬��D��AB���ϵ�һ�㣬��D����BC�Ĵ��ߣ�����Ϊ��E����֪��AB=4cm��BC=8cm��CD=7cm�����DBE���ܳ�Ϊ��������| A�� | 5cm | B�� | 6cm | C�� | $\frac{9+3\sqrt{3}}{2}$cm | D�� | 8cm |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com