
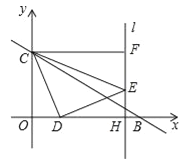
【题目】在平面直角坐标系中,直线![]() 与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m.
与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m.
(1)请直接写出点B、C的坐标;
(2)当点E落在直线BC上时,求tan∠FDE的值;
(3)对于常数m,探究:在直线l上是否存在点G,使得∠CDO=∠DFE+∠DGH?若存在,请求出点G的坐标;若不存在,请说明理由.
【答案】(1)B(5,0),C(0,3);(2)![]() ;(3)当0<m<3时,存在∠CDO=∠DFE+∠DGH,此时G(3+m,
;(3)当0<m<3时,存在∠CDO=∠DFE+∠DGH,此时G(3+m,![]() )或(3+m,﹣
)或(3+m,﹣![]() ).
).
【解析】
试题分析:(1)分别令x=0和y=0,即可求得;
(2)证得四边形COHF是矩形,然后证得△OCD≌△HDE,从而证得△DHF是等腰直角三角形,得出∠HDE+∠FDE=45°,由∠OCD+∠ECF=45°,得出∠ECF=∠FDE,进一步得出∠OBC=∠FDE,解直角三角形即可求得tan∠OBC=![]() =
=![]() ,从而得出tan∠FDE=
,从而得出tan∠FDE=![]() .
.
(3)根据三角形全等的性质要使∠CDO=∠DFE+∠DGH,只要△EDF∽△EGD,所以只要![]() ,即DE2=EFEG,由(2)可知:DE2=CD2=OD2+OC2=m2+32,EF=3﹣m,然后分三种情况讨论即可求得.
,即DE2=EFEG,由(2)可知:DE2=CD2=OD2+OC2=m2+32,EF=3﹣m,然后分三种情况讨论即可求得.
试题解析:(1)∵直线![]() 与x轴、y轴相交于B、C两点,∴令y=0,则0=
与x轴、y轴相交于B、C两点,∴令y=0,则0=![]() ,解得x=5,令x=0,则y=3,∴B(5,0),C(0,3);
,解得x=5,令x=0,则y=3,∴B(5,0),C(0,3);
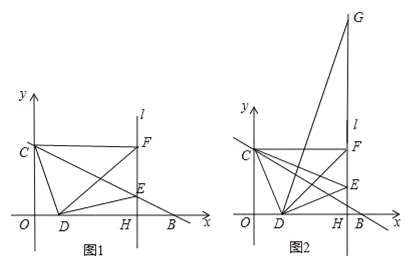
(2)如图1,∵∠CDE=90°,∴∠CDO+∠EDH=90°,∵∠CDO+∠OCD=90°,∴∠OCD=∠EDH,在△OCD和△HDE中,∵∠OCD=∠HDE,∠COD=∠DHE=90°,CD=DE,∴△OCD≌△HDE(AAS),∴DH=OC=3,∵直线l⊥x轴于H,CF⊥y轴,∴四边形COHF是矩形,∴FH=OC=3,∴DH=HF,∴∠HDF=45°,即∠HDE+∠FDE=45°,∵CD=DE,∠CDE=90°,∴∠DCE=45°,∴∠OCD+∠ECF=45°,∴∠ECF=∠FDE,∵∠OBC=∠ECF,∵tan∠OBC=![]() =
=![]() ,∴tan∠FDE=
,∴tan∠FDE=![]() .
.
(3)如图2,由(2)可知△OCD≌△HDE,∴∠CDO=∠DEH,要使∠CDO=∠DFE+∠DGH,只要∠DEH=∠DFE+∠DGH,在△DEF中,∠DEH=∠EDF+∠DFE,∴只要∠EDF=∠DGF,∵∠FED=∠GED,只要△EDF∽△EGD,∴只要![]() ,即DE2=EFEG,由(2)可知:DE2=CD2=OD2+OC2=m2+32,EF=3﹣m,∴当0<m<3时,EG=
,即DE2=EFEG,由(2)可知:DE2=CD2=OD2+OC2=m2+32,EF=3﹣m,∴当0<m<3时,EG=![]() =
=![]() ,HO=3+m,此时,G(3+m,
,HO=3+m,此时,G(3+m,![]() ),根据对称可知,当0<m<3时,此时还存在G′(3+m,﹣
),根据对称可知,当0<m<3时,此时还存在G′(3+m,﹣![]() );
);
当m=3时,此时点E和点F重合,∠DFE不存在,当3≤m≤5时,点E在F的上方,此时,∠DFE>∠DEF,此时不存在∠CDO=∠DFE+∠DGH,综上,当0<m<3时,存在∠CDO=∠DFE+∠DGH,此时G(3+m,![]() )或(3+m,﹣
)或(3+m,﹣![]() ).
).


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如表:
(1)把表中所空各项数据填写完整;
选手 | 选拔成绩/环 | 中位数 | 平均数 | |||||
甲 | 10 | 9 | 8 | 8 | 10 | 9 | ||
乙 | 10 | 10 | 8 | 10 | 7 | 9 | ||
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一天中售出李宁牌运动鞋11双,其中各种尺码的鞋的销售量如表所示,则这11双鞋的尺码组成一组数据中位数为_____.
鞋的尺码(单位:厘米) | 23.5 | 24 | 24.5 | 25 | 26 |
销售量(单位:双) | 1 | 2 | 2 | 5 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图(1),在△ABC中,已知AB=AC,BE=CF.
(1)发现问题:小华审题后发现,若连接CE,BF,则CE=BF,请说明理由;
(2)提出问题:如图(2),设CE与BF交于点O,则直线AO是BC边的垂直平分线吗?试说明理由;
(3)解决问题:在图(3)中,是各边相等,各内角也相等的正五边形ABCDE,请你只用无刻度的直尺画出图中BC边的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
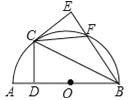
【题目】如图,以AB为直径作半圆O,点C为半圆上与A,B不重合的一动点,过点C作CD⊥AB于点D,点E与点D关于BC对称,BE与半圆交于点F,连CE.
(1)判断CE与半圆O的位置关系,并给予证明.
(2)点C在运动时,四边形OCFB的形状可变为菱形吗?若可以,猜想此时∠AOC的大小,并证明你的结论;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
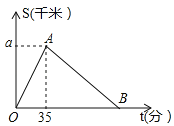
【题目】2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回中点万地广场西门.设该运动员离开起点的路程S(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米/分,用时35分钟,根据图象提供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点C,该运动员从第一次经过C点到第二次经过C点所用的时间为68分钟.
①求AB所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com