
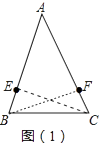
【题目】问题背景:如图(1),在△ABC中,已知AB=AC,BE=CF.
(1)发现问题:小华审题后发现,若连接CE,BF,则CE=BF,请说明理由;
(2)提出问题:如图(2),设CE与BF交于点O,则直线AO是BC边的垂直平分线吗?试说明理由;
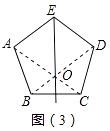
(3)解决问题:在图(3)中,是各边相等,各内角也相等的正五边形ABCDE,请你只用无刻度的直尺画出图中BC边的垂直平分线.
【答案】
(1)解:如图1中,连接EC、BF.
∵AB=AC,
∴∠ABC=∠ACB,
在△EBC和△FCB中,
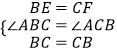 ,
,
∴△EBC≌△FCB,
∴CE=BF;
(2)解:结论:AO是BC边的中垂线,
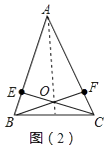
理由:∵△EBC≌△FCB,
∴∠OEB=∠OFC,
在△EOB和△FOC中,
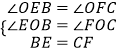 ,
,
∴△EOB≌△FOC,
∴OB=OC,又AB=AC,
∴AO是BC边的中垂线
(3)解:如图(3):连接AC、BD交于点O,作直线EO,直线EO即为线段BC的垂直平分线.
【解析】(1)首先依据等腰三角形的性质得到∠ABC=∠ACB,然后再依据SAS证明△EBC≌△FCB即可;
(2)证明△EOB≌△FOC,得到OB=OC,根据线段垂直平分线的判定定理得到答案;
(3)根据点到线段的两个端点的距离相等的点在线段的垂直平分线上作图即可.
【考点精析】关于本题考查的等腰三角形的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
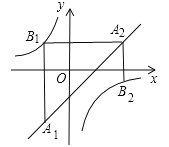
【题目】如图,已知点A1,A2,…,An均在直线![]() 上,点B1,B2,…,Bn均在双曲线
上,点B1,B2,…,Bn均在双曲线![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若![]() ,则a2015= .
,则a2015= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某绿色食品有限公司准备购进A和B两种蔬菜,B种蔬菜每吨的进价比A中蔬菜每吨的进价多0.5万元,经计算用4.5万元购进的A种蔬菜的吨数与用6万元购进的B种蔬菜的吨数相同,请解答下列问题:
(1)求A,B两种蔬菜每吨的进价;
(2)该公司计划用14万元同时购进A,B两种蔬菜,若A种蔬菜以每吨2万元的价格出售,B种蔬菜以每吨3万元的价格出售,且全部售出,请求出所获利润W(万元)与购买A种蔬菜的资金a(万元)之间的函数关系式;
(3)在(2)的条件下,要求A种蔬菜的吨数不低于B种蔬菜的吨数,若公司欲将(2)中的最大利润全部用于购买甲、乙两种型号的电脑赠给某中学,甲种电脑每台2100元,乙种电脑每台2700元,请直接写出有几种购买电脑的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
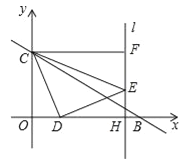
【题目】在平面直角坐标系中,直线![]() 与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m.
与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m.
(1)请直接写出点B、C的坐标;
(2)当点E落在直线BC上时,求tan∠FDE的值;
(3)对于常数m,探究:在直线l上是否存在点G,使得∠CDO=∠DFE+∠DGH?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.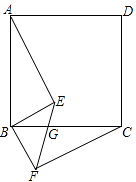
(1)求证:AE=CF;
(2)若∠ABE=65°,求∠EGC的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com