
【题目】有一块形状为四边形的钢板,量得它的各边长度为AB=9cm,BC=12cm,CD=17cm,DA=8cm,∠B=90°.求这块钢板的面积. 
【答案】解:连接AC,在RT△ABC中,AC= ![]() =15,在△ADC中,AD=8cm,CD=17cm,
=15,在△ADC中,AD=8cm,CD=17cm,
则AC2+AD2=DC2 ,
故可得△ADC为直角三角形,
这块钢板的面积=S△ABC+S△ADC= ![]() AB×BC+
AB×BC+ ![]() AD×AC=54+60=114
AD×AC=54+60=114
【解析】连接AC,在RT△ABC中,利用可勾股定理可得出AC,利用勾股定理的逆定理可判断△ADC是直角三角形,分别求出两个直角三角形的面积相加即可.
【考点精析】通过灵活运用勾股定理的概念和勾股定理的逆定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形即可以解答此题.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】某公园的成人票价是15元,儿童买半票,甲旅行团有x(名)成年人和y(名)儿童,乙旅行团的成人数是甲旅行团的2倍,儿童数比甲旅行团的2倍少8人.这两个旅行团的门票费用总和各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图(1),在△ABC中,已知AB=AC,BE=CF.
(1)发现问题:小华审题后发现,若连接CE,BF,则CE=BF,请说明理由;
(2)提出问题:如图(2),设CE与BF交于点O,则直线AO是BC边的垂直平分线吗?试说明理由;
(3)解决问题:在图(3)中,是各边相等,各内角也相等的正五边形ABCDE,请你只用无刻度的直尺画出图中BC边的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列题目.
(1)求: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() 的值. 对于这个问题,可能有的同学接触过,一般方法是考虑其中的一般项,注意到上面和式的每一项可以写成
的值. 对于这个问题,可能有的同学接触过,一般方法是考虑其中的一般项,注意到上面和式的每一项可以写成 ![]() 的形式,而
的形式,而 ![]() =
= ![]() ﹣
﹣ ![]() ,这样就把
,这样就把 ![]() 一项(分)裂成了两项.
一项(分)裂成了两项.
试着把上面和式的每一项都裂成两项,注意观察其中的规律,求出上面的和,并直接写出 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() 的值.
的值.
(2)若 ![]() =
= ![]() +
+ ![]() ①求:A、B的值:
①求:A、B的值:
②求: ![]() +
+ ![]() +…+
+…+ ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠BAC=90°,将△ABC沿直线BC向右平移得到△DEF,连结AD、AE,则下列结论中不成立的是( )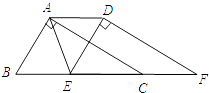
A.AD∥BE,AD=BE
B.∠ABE=∠DEF
C.ED⊥AC
D.△ADE为等边三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com