Question

12．如图①，南京中山陵的台阶拾级而上被分成坡度不等的两部分．图②是台阶的侧面图，若斜坡BC长为120m，在C处看B处的仰角为25°；斜坡AB长70m，在A处看B处的俯角为50°，试求出陵墓的垂直高度AE的长．
（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19，sin25°≈0.42，cos25°≈0.91，tan25°≈0.47）

Answer 1

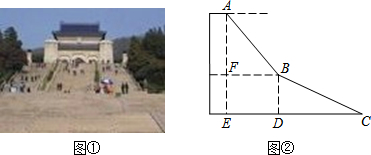
分析 在Rt△BDC中，根据sinC=$\frac{BD}{BC}$，求出BD的长，然后在Rt△AFB中，根据sin∠ABF=$\frac{AF}{AB}$，求出AF的长，进而求出AE的长．

解答 解：在Rt△BDC中，sinC=$\frac{BD}{BC}$，
∴BD=BC•sinC=BC•sin25°=120×0.42=50.4 m．
在Rt△AFB中，sin∠ABF=$\frac{AF}{AB}$，
∴AF=AB•sin∠ABF=AB•sin50°=70×0.77=53.9 m．
∴AE=AF+FE=AF+BD=50.4+53.9=104.3m．
答：陵墓的垂直高度AE的长为104.3 m．

点评 本题考查了解直角三角形的应用--仰角、俯角问题，要求学生能借助仰角构造直角三角形并解直角三角形．